题目内容
13.已知函数f(x)=$\frac{|x|}{x+2}$,如果关于x的方程f(x)=kx2有四个不同的实数解,则k的取值范围是( )| A. | k>1 | B. | k≥1 | C. | 0<k<1 | D. | 0<k≤1 |
分析 根据方程的特点,相当于只需有三个不等于零的不同实数根,把方程解的问题转化为两函数的交点问题,通过数形结合得出k的范围.
解答  解:f(x)=kx2有四个不同的实数解,
解:f(x)=kx2有四个不同的实数解,
∴显然当x=0时,无论k为何值,都成立,
当只需有三个不等于零的不同实数根,
∴方程可化$\frac{1}{k}$=|x|(x+2),
只需y=$\frac{1}{k}$和y=|x|(x+2)有三个不等于零的交点即可,画出函数y=|x|(x+2)的图象如图:
有图象可知只需0<$\frac{1}{k}$<1,
∴k>1,
故选A.
点评 本题考查了方程的解和函数的交点问题的转换,难点是利用数形结合的思想解决问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.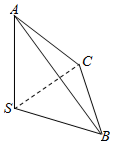 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
8.在数列{an}中,a7=16,an-$\frac{1}{2}$an+1=0,则a2的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
18.若α,β都是锐角,且$sinα=\frac{2\sqrt{5}}{5},sin(α-β)=\frac{\sqrt{10}}{10}$,则cosβ=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{2}$或$-\frac{\sqrt{2}}{10}$ | D. | $\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{10}$ |
2.$cos\frac{2π}{3}•tan\frac{7π}{4}$的值为( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
3.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数f(x)=x2+2ax+2有两个不同零点的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
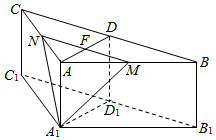 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.