题目内容
11.已知函数f(x)的定义域为D,若对于?a,b,c∈D,.f(a),f (b),f(c)分别为某个三角形的三边长,则称f(x)为“三角形函数”.给出下列四个函数:①f(x)=lnx(x>1)
②f(x)=4+sinx
③f(x)=${x^{\frac{1}{3}}}$(1≤x≤8)
④f(x)=$\frac{{{2^x}+2}}{{{2^x}+1}}$
其中为“三角形函数”的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设它的三边长分别为a,b,c,则a+b>c,若f(x)为“三角形函数,则满足f(a)+f(b)>f(c)或者f(x)max-f(x)min<f(x)min,即可.
解答 ②任给三角形,设它的三边长分别为a,b,c,则a+b>c,
不妨假设a≤c,b≤c,
设a=1.1,b=1.1,c=2时,满足a+b>c,
由于lna+lab=ln(ab)=ln1.21>ln2不成立,
所以h(x)=lnx,x∈[1,+∞)不是为三角形函数”;
②f(x)=4+sinx的最大值f(x)max=4+1=5,最小值f(x)min=4-1=3,则f(x)max-f(x)min=5-3=2<f(x)min,即函数f(x)=4+sinx为“三角形函数”.
③f(x)=${x^{\frac{1}{3}}}$(1≤x≤8)为增函数,则最大值f(x)max=${8}^{\frac{1}{3}}=\root{3}{8}$=2,最小值f(x)min=1,则f(x)max-f(x)min=2-1<1不成立,即函数f(x)=${x^{\frac{1}{3}}}$(1≤x≤8)
不是“三角形函数”.
④f(x)=$\frac{{{2^x}+2}}{{{2^x}+1}}$=$\frac{{2}^{x}+1+1}{{2}^{x}+1}$=1+$\frac{1}{{2}^{x}+1}$,则f(x)∈(1,2),最大值f(x)max<2,f(x)min>1,则f(x)max-f(x)min<1,则f(x)max-f(x)min<f(x)min成立,
故f(x)=$\frac{{{2^x}+2}}{{{2^x}+1}}$是“三角形函数”,
故是“三角形函数”的是②④,
故选:B
点评 本题主要考查命题的真假判断,涉及新定义“三角形函数”,根据条件转化为求f(x)max-f(x)min<f(x)min,是解决本题的关键.综合性较强,难度较大.

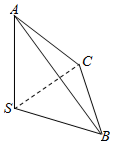 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | p为真 | B. | ¬q为假 | C. | p∧q为真 | D. | p∨q为假 |
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |