题目内容
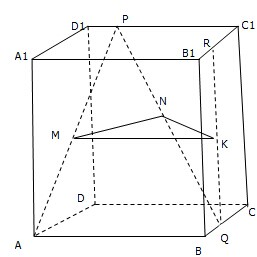如图，在正方体ABCD-A1B1C1D1中，P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点，M、N、K分别为线段AP、PQ、QR的中点，求证：平面MNK∥平面ABCD．考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：要证面面平行，可以通过相交直线平行于相交直线，即通过MN∥AQ，NK∥HQ进行转化，中位线定理在解答中期关键作用．
解答：
证明：，在正方体ABCD-A1B1C1D1中，连接AQ，PR在平面ABCD中作PR∥HQ
∵P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点，M、N、K分别为线段AP、PQ、QR的中点．
∴MN∥AQ NK∥PR
∵PR∥HQ
∴NK∥HQ
平面MNK∥平面ABCD
∵P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点，M、N、K分别为线段AP、PQ、QR的中点．
∴MN∥AQ NK∥PR
∵PR∥HQ
∴NK∥HQ
平面MNK∥平面ABCD
点评：本题考查的知识点：面面平行的判定定理，三角形的中位线定理，属于基础题型．
练习册系列答案
相关题目
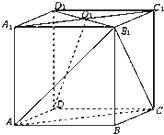已知正方体ABCD-A1B1C1D1中，面A1B1C1D1中心为O1．
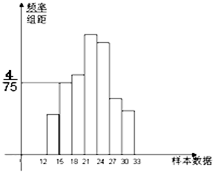如图是总体的一个样本频率分布直方图，且在[15，18）内频数为8，在[12，15）内的小矩形面积为0.1．