题目内容
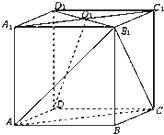 已知正方体ABCD-A1B1C1D1中,面A1B1C1D1中心为O1.
已知正方体ABCD-A1B1C1D1中,面A1B1C1D1中心为O1.(1)求证:DO1∥面AB1C;
(2)求异面直线DO1与B1C所成角.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:平面向量及应用,空间位置关系与距离
分析:(1)建立如图所示的直角坐标系.利用向量垂直与数量积的关系求出平面AB1C的法向量
,只要证明
•
=0即可;
(2)利用向量的夹角公式即可得出.
| n |
| DO1 |
| n |
(2)利用向量的夹角公式即可得出.
解答:
解:(1)证明:建立如图所示的直角坐标系.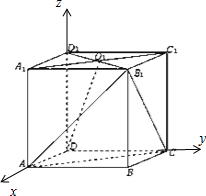
设AB=2,O1(1,1,2),A(2,0,0),B1(2,2,2),
C(0,2,0).
=(1,1,2),
=(-2,2,0),
=(0,2,2).
设平面AB1C的法向量为
=(x,y,z),
则
,化为
,令y=1,解得x=1,z=-1.
∴
=(1,1,-1),
∵
•
=1+1-2=0,∴
⊥
,
∵点D∉平面AB1C,∴DO1∥面AB1C;
(2)
=(-2,0,-2),
cos<
,
>=
=
=-
,
∴<
,
>=150°,
∴异面直线DO1与B1C所成角为30°.

设AB=2,O1(1,1,2),A(2,0,0),B1(2,2,2),
C(0,2,0).
| DO1 |
| AC |
| AB1 |
设平面AB1C的法向量为
| n |
则
|
|
∴
| n |
∵
| DO1 |
| n |
| n |
| DO1 |
∵点D∉平面AB1C,∴DO1∥面AB1C;
(2)
| B1C |
cos<
| DO1 |
| B1C |
| ||||
|
|
| -6 | ||||
|
| ||
| 2 |
∴<
| DO1 |
| B1C |
∴异面直线DO1与B1C所成角为30°.
点评:本题考查了向量垂直与数量积的关系、线面垂直与线面平行的判定定理、异面直线所成的角,考查了空间想象能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
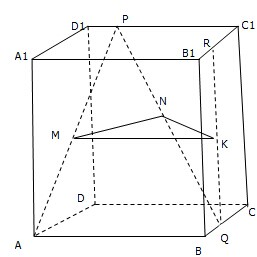 如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.
如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.