题目内容
袋子中装有标号为1,2,3,4的四个球,从中随机取出2个,用X表示所取出的两个球的标号之和.
(1)求所取出的两个球的标号之和等于5的概率.
(2)求随机变量X的分布列.
(1)求所取出的两个球的标号之和等于5的概率.
(2)求随机变量X的分布列.
考点:离散型随机变量及其分布列,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)袋子中装有标号为1,2,3,4的四个球,从中随机取出2个,基本事件总数n=
=6,所取出的两个球的标号之和等于5,包含2个基本事件,所取出的两个球的标号之和等于5的概率.
(2)由题意知X的所有可能取值为3,4,5,6,7,分别求出相应的概率,由此能求出X的分布列.
| C | 2 4 |
(2)由题意知X的所有可能取值为3,4,5,6,7,分别求出相应的概率,由此能求出X的分布列.
解答:
解:(1)袋子中装有标号为1,2,3,4的四个球,从中随机取出2个,
基本事件总数n=
=6,
所取出的两个球的标号之和等于5,包含2个基本事件,
∴所取出的两个球的标号之和等于5的概率:
p=
=
.
(2)由题意知X的所有可能取值为3,4,5,6,7,
P(X=3)=
,
P(X=4)=
,
P(X=5)=
,
P(X=6)=
,
P(X=7)=
,
∴X的分布列为:
基本事件总数n=
| C | 2 4 |
所取出的两个球的标号之和等于5,包含2个基本事件,
∴所取出的两个球的标号之和等于5的概率:
p=
| 2 |
| 6 |
| 1 |
| 3 |
(2)由题意知X的所有可能取值为3,4,5,6,7,
P(X=3)=
| 1 |
| 6 |
P(X=4)=
| 1 |
| 6 |
P(X=5)=
| 2 |
| 6 |
P(X=6)=
| 1 |
| 6 |
P(X=7)=
| 1 |
| 6 |
∴X的分布列为:
| X | 3 | 4 | 5 | 6 | 7 | ||||||||||
| P |
|
|
|
|
|
点评:本题考查概率的求法,考查离散型随机变量的分布列的求法,解题时要认真审题,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
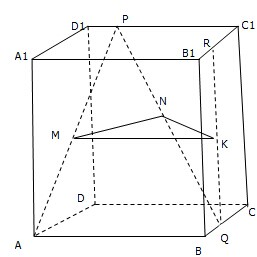 如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.
如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.