题目内容
已知函数f(x)=
,求f(x)的值域.
|
考点:函数的值域
专题:函数的性质及应用
分析:对每一段二次函数进行配方,即可求出f(x)在每段上的范围,从而求得f(x)的值域.
解答:
解:f(x)=
;
∴0≤x≤3时,f(x)∈[-4,0];
-2≤x≤0时,f(x)∈[-8,0];
∴f(x)的值域为[-8,0].
|
∴0≤x≤3时,f(x)∈[-4,0];
-2≤x≤0时,f(x)∈[-8,0];
∴f(x)的值域为[-8,0].
点评:考查函数的值域及求分段函数值域的方法:在每段上求函数的值域,再求并集,而对于涉及二次函数的值域时,一般用配方法较容易.

练习册系列答案
相关题目
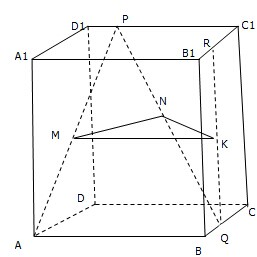 如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.
如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.