题目内容
已知平面向量
=(cosx,sinx),
=(2sinx,-2cosx),
=
+m
,
=cos2x•
+sinx•
,f(x)=
•
,x∈R.
(1)当m=2时,求y=f(x)的取值范围;
(2)若f(x)的最大值是7,求实数m的值.
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
(1)当m=2时,求y=f(x)的取值范围;
(2)若f(x)的最大值是7,求实数m的值.
考点:三角函数的最值
专题:三角函数的求值,平面向量及应用
分析:(1)由条件利用两个向量的数量积公式求得f(x)═-2(sinx-m)2+1+2m2.令t=sinx,则-1≤t≤1,则f(x)=h(t)=-2(t-m)2+1+2m2.再利用二次函数的性质求得
f(x)=h(t)的范围.
(2)分对称轴t=m在区间的左侧、中间、右侧三种情况,分别根据最大值为7求得m的值,综合可得结论.
f(x)=h(t)的范围.
(2)分对称轴t=m在区间的左侧、中间、右侧三种情况,分别根据最大值为7求得m的值,综合可得结论.
解答:
解:(1)由题意知|
|=1,|
|=2,
•
=0,f(x)=
•
=cos2x
2+msinx
2=cos2x+4msinx=-2sin2x+4msinx+1=-2(sinx-m)2+1+2m2.
令t=sinx,则-1≤t≤1,则f(x)=h(t)=-2(t-m)2+1+2m2.
当m=2时,h(t)=-2(t-2)2+9在[-1,1]上递增,则h(t)∈[h(-1),h(1)],即h(t)的范围[-9,7];
(2)①当m<-1时,h(t)=-2(t-m)2+1+2m2在[-1,1]上单调递减,h(t)max=h(-1)=-4m-1;-4m-1=7,所以m=-2满足条件;
②当-1≤m≤1时,h(t)=-2(t-m)2+1+2m2在[-1,1]上先增后减,h(t)max=h(m)=2m2+1;2m2+1=7,则m=±
不满足条件;
③当m>1时,h(t)=-2(t-m)2+1+2m2在[-1,1]上单调递增,h(t)max=h(1)=4m-1;4m-1=7,所以m=2满足条件;
综上,m=±2.
| a |
| b |
| a |
| b |
| c |
| d |
| a |
| b |
令t=sinx,则-1≤t≤1,则f(x)=h(t)=-2(t-m)2+1+2m2.
当m=2时,h(t)=-2(t-2)2+9在[-1,1]上递增,则h(t)∈[h(-1),h(1)],即h(t)的范围[-9,7];
(2)①当m<-1时,h(t)=-2(t-m)2+1+2m2在[-1,1]上单调递减,h(t)max=h(-1)=-4m-1;-4m-1=7,所以m=-2满足条件;
②当-1≤m≤1时,h(t)=-2(t-m)2+1+2m2在[-1,1]上先增后减,h(t)max=h(m)=2m2+1;2m2+1=7,则m=±
| 6 |
③当m>1时,h(t)=-2(t-m)2+1+2m2在[-1,1]上单调递增,h(t)max=h(1)=4m-1;4m-1=7,所以m=2满足条件;
综上,m=±2.
点评:本题主要考查两个向量的数量积公式、二次函数的性质的应用,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
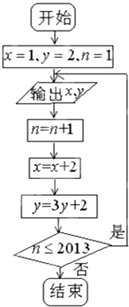 根据如图的程序框图,将输出的x,y值依次分别记为x1,x2,…,x2013;y1,y2…y2013
根据如图的程序框图,将输出的x,y值依次分别记为x1,x2,…,x2013;y1,y2…y2013