题目内容
已知等比数列{an}，S20=21，S30=49，则S10= ．
考点：等比关系的确定
专题：等差数列与等比数列
分析：本题可以利用等比数列的前n项和、次n项和、再n项和成等比，得到本题结论．
解答：
解：∵数列{an}中，S20=21，S30=49，
∴a21+a22+…+a30=S30-S20=49-21=28≠0．
又∵等比数列{an}，
∴a1+a2+…+a10，a11+a12+…+a20，a21+a22+…+a30成等比，
即S10，S20-S10，S30-S20成等比，
∴(21-S10)2=S10×(49-21)．
∴S10=7．
故答案为7．
∴a21+a22+…+a30=S30-S20=49-21=28≠0．
又∵等比数列{an}，
∴a1+a2+…+a10，a11+a12+…+a20，a21+a22+…+a30成等比，
即S10，S20-S10，S30-S20成等比，
∴(21-S10)2=S10×(49-21)．
∴S10=7．
故答案为7．
点评：本题考查的等比数列的派生数列，本题应用时要注意和不为0，本题的一定的思维难度，属于中档题．
练习册系列答案
优加精卷系列答案
相关题目
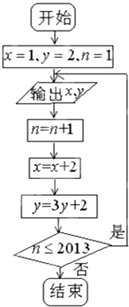根据如图的程序框图，将输出的x，y值依次分别记为x1，x2，…，x2013；y1，y2…y2013