题目内容
将进货单价为80元的商品按90元一个售出时，能卖出400个，已知这种商品每个涨价1元，其销售量就减少10个，为了取得最大利润，每个售价应定为多少元？
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用
分析：假设售价在90元的基础上涨x元，从而得到销售量，进而可以构建函数关系式，利用二次函数求最值的方法求出函数的最值．
解答：
解：设售价在90元的基础上涨x元
因为这种商品每个涨价1元，其销售量就减少10个，所以若涨x元，则销售量减少10x，按90元一个能全部售出，则按90+x元售出时，能售出400-10x个，每个的利润是90+x-80=10+x元
设总利润为y元，则y=（10+x）（400-10x）=-10x2+300x+4000，对称轴为x=15
所以x=15时，y有最大值，售价则为105元
所以售价定为每个105元时，利润最大．
因为这种商品每个涨价1元，其销售量就减少10个，所以若涨x元，则销售量减少10x，按90元一个能全部售出，则按90+x元售出时，能售出400-10x个，每个的利润是90+x-80=10+x元
设总利润为y元，则y=（10+x）（400-10x）=-10x2+300x+4000，对称轴为x=15
所以x=15时，y有最大值，售价则为105元
所以售价定为每个105元时，利润最大．
点评：本题考查函数模型的构建，考查求二次函数的最值，解题的关键是读懂题意，列出函数解析式．
练习册系列答案
相关题目
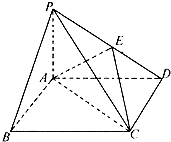四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，E是侧棱PD的中点．
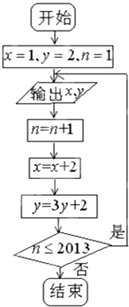根据如图的程序框图，将输出的x，y值依次分别记为x1，x2，…，x2013；y1，y2…y2013