题目内容
已知凼数f(x)=
(a∈R),曲线y=f(x)在点(1,f(1))处的切线方程为y=x-1
(1)求实数a的值,并求f(x)的单调区间
(2)是否存在k∈Z,使得kx>f(x)+2对任意x>0恒成立?若存在,求出k的最小值,若不存在,请说明理由
(3)试比较20142015与20152014的大小,并说明理由.
| lnx |
| x+a |
(1)求实数a的值,并求f(x)的单调区间
(2)是否存在k∈Z,使得kx>f(x)+2对任意x>0恒成立?若存在,求出k的最小值,若不存在,请说明理由
(3)试比较20142015与20152014的大小,并说明理由.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)利用导数的运算法则可得f′(x)=
,(x>0).再利用几何意义可得f′(1)=1即可解得a.再利用导数研究其单调性,分别解出f′(x)<0,f′(x)>0,即可得出其单调区间.
(2)若kx>f(x)+2对任意x>0恒成立,则k>
+
,记g(x)=
+
,只需k>g(x)max.利用导数研究其最大值即可得出.
(3)由(1)可得:函数f(x)=
在x>1时单调递减.可得
<
,化简整理即可得出.
| (x+a)-xlnx |
| x(x+a)2 |
(2)若kx>f(x)+2对任意x>0恒成立,则k>
| lnx |
| x2 |
| 2 |
| x |
| lnx |
| x2 |
| 2 |
| x |
(3)由(1)可得:函数f(x)=
| lnx |
| x |
| ln2015 |
| 2015 |
| ln2014 |
| 2014 |
解答:
解:(1)f′(x)=
,(x>0).∵曲线y=f(x)在点(1,f(1))处的切线方程为y=x-1,
∴f′(1)=
=1,解得a=0.
∴f(x)=
.
f′(x)=
,
当x>e时,f′(x)<0,此时函数f(x)单调递减;当0<x<e时,f′(x)>0,此时函数f(x)单调递增.
∴函数f(x)单调递减区间为(e,+∞);函数f(x)单调递增区间为(0,e).
(2)若kx>f(x)+2对任意x>0恒成立,则k>
+
,
记g(x)=
+
,只需k>g(x)max.
又g′(x)=
-
=
,
记h(x)=1-2x-2lnx(x>0),则h′(x)=-2-
<0,
所以h(x)在(0,+∞)上单调递减.
又h(1)=-1<0,h(
)=1-
-2ln
>1-
+ln2=lnln
>0,
∴存在唯一x0∈(
,1),使得h(x0)=0,即1-2x0-2lnx0=0,
当x>0时,h(x)、g′(x)、g(x)的变化情况如下:
∴g(x)max=g(x0)=
,
又∵1-2x0-2lnx0=0,∴2x0+2lnx0=1,
∴g(x0)=
=
=
(
)2+
,
∵x0∈(
,1),∴
∈(1,
),∴
<g(x0)<1+
.
又g(x)max≥g(1)=2,∴2≤g(x0)<1+
.
∵k>g(x)max,即k>g(x0),且k∈Z,故k的最小整数值为3.
存在最小整数k=3,使得kx>f(x)+2对任意x>0恒成立.
(3)由(1)可得:函数f(x)=
在x>1时单调递减.
∴
<
,
即ln20152014<ln20142015,
∴20152014<20142015.
| (x+a)-xlnx |
| x(x+a)2 |
∴f′(1)=
| 1+a |
| (1+a)2 |
∴f(x)=
| lnx |
| x |
f′(x)=
| 1-lnx |
| x2 |
当x>e时,f′(x)<0,此时函数f(x)单调递减;当0<x<e时,f′(x)>0,此时函数f(x)单调递增.
∴函数f(x)单调递减区间为(e,+∞);函数f(x)单调递增区间为(0,e).
(2)若kx>f(x)+2对任意x>0恒成立,则k>
| lnx |
| x2 |
| 2 |
| x |
记g(x)=
| lnx |
| x2 |
| 2 |
| x |
又g′(x)=
| 1-2lnx |
| x3 |
| 2 |
| x2 |
| 1-2x-2lnx |
| x3 |
记h(x)=1-2x-2lnx(x>0),则h′(x)=-2-
| 2 |
| x |
所以h(x)在(0,+∞)上单调递减.
又h(1)=-1<0,h(
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 | ||
|
∴存在唯一x0∈(
| ||
| 2 |
当x>0时,h(x)、g′(x)、g(x)的变化情况如下:
| x | (0,x0) | x0 | (x0,+∞) |
| h(x) | + | 0 | - |
| g′(x) | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
| 2x0+lnx0 | ||
|
又∵1-2x0-2lnx0=0,∴2x0+2lnx0=1,
∴g(x0)=
| (2x0+2lnx0)+2x0 | ||
2
|
| 1+2x0 | ||
2
|
| 1 |
| 2 |
| 1 |
| x0 |
| 1 |
| x0 |
∵x0∈(
| ||
| 2 |
| 1 |
| x0 |
| 2 |
| 3 |
| 2 |
| 2 |
又g(x)max≥g(1)=2,∴2≤g(x0)<1+
| 2 |
∵k>g(x)max,即k>g(x0),且k∈Z,故k的最小整数值为3.
存在最小整数k=3,使得kx>f(x)+2对任意x>0恒成立.
(3)由(1)可得:函数f(x)=
| lnx |
| x |
∴
| ln2015 |
| 2015 |
| ln2014 |
| 2014 |
即ln20152014<ln20142015,
∴20152014<20142015.
点评:本题考查了利用导数研究函数的单调性极值最值、恒成立问题的等价转化方法,考查了利用已经证明的结论证明不等式的方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在三棱锥A-BCD的各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )
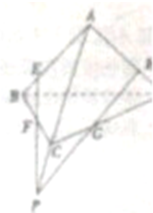

| A、一定在直线BD上 |
| B、一定在直线AC上 |
| C、在直线AC或BD上 |
| D、不在直线AC上,也不在直线BD上 |
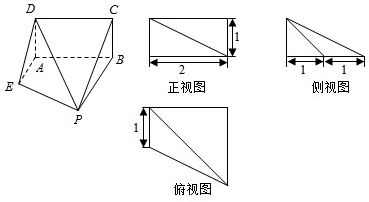
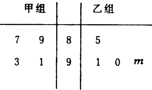 如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示.
如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示. 如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若
如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若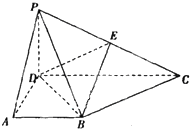 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.