Question

已知一个空间几何体的直观图和三视图（尺寸如图所示）．

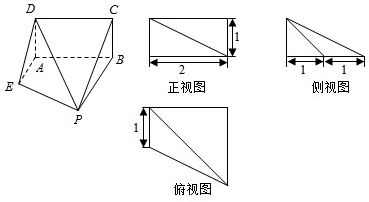
（Ⅰ）设点M为棱PD中点，求证：EM∥平面ABCD；
（Ⅱ）线段PD上是否存在一点N，使得直线BN与平面PCD所成角的正弦值等于

2

5

？若存在，试确定点N的位置；若不存在，请说明理由．

Answer 1

考点：直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）以B为原点，

BA

，

BP

，

BC

分别为x轴，y轴，z轴正方向，建立如图所示的空间直角坐标系，求出平面ABCD的一个法向量，由此能证明EM∥平面ABCD．
（Ⅱ）求出平面PCD的法向量和平面PCD的一个法向量，由此利用向量法能求出线段PD上存在一点N，当N点与D点重合时，直线BN与平面PCD所成角的正弦值等于

2

5

．

解答： 解：（Ⅰ）证明：由三视图知，BA，BP，BC两两垂直，故以B为原点，

BA

，

BP

，

BC

分别为x轴，y轴，z轴正方向，
建立如图所示的空间直角坐标系．…（1分）
则P（0，2，0），D（2，0，1），M（1，1，

1

2

），E（2，1，0），C（0，0，1），
所以

EM

=（-1，0，

1

2

），
平面ABCD的一个法向量等于

n

=（0，1，0），…（3分）
所以

EM

•

n

=(-1，0，

1

2

)•(0，1，0)=0，所以

EM

⊥

n

，（4分）
又EM?平面ABCD，所以EM∥平面ABCD．（5分）
（Ⅱ）解：当点N与点D重合时，直线BN与平面PCD所成角的正弦值为

2

5

．（6分）
理由如下：
因为

PD

=(2，-2，1)，

CD

=（2，0，0），设平面PCD的法向量为

n

=（x，y，z），
由

n • PD =2x-2y+z=0 n • CD =2x=0

，（7分）
取y=1，得平面PCD的一个法向量

n

=（0，1，2）．（8分）
假设线段PD上存在一点N，使得直线BN与平面PCD所成角α的正弦值等于

2

5

．
设

PN

=λ

PD

（0≤λ≤1），
则

PN

=λ(2，-2，1)=(2λ，-2λ，λ)，

BN

=

BP

+

PN

=（2λ，2-2λ，λ）．（9分）
所以sinα=|cos＜

BN

，

n

＞|=

| BN ， n |

| BN |•| n |

（10分）
=

2

5 • (2λ)2+(2-2λ)2+λ2

=

2

5 • 9λ2-8λ+4

=

2

5

．（12分）
所以9λ²-8λ-1=0，解得λ=1，或λ=-

1

9

．（舍去）．
因此，线段PD上存在一点N，当N点与D点重合时，
直线BN与平面PCD所成角的正弦值等于

2

5

． （13分）

点评：本题考查考查直线与平面的平行、线面所成角、探索性问题等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查数形结合思想、化归与转化思想、函数与方程思想．