题目内容
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,c=\sqrt{{a^2}-{b^2}},e=\frac{c}{a})$,其左、右焦点分别为F1,F2,关于椭圆有以下四种说法:(1)设A为椭圆上任一点,其到直线${l_1}:x=-\frac{a^2}{c},{l_2}:x=\frac{a^2}{c}$的距离分别为d2,d1,则$\frac{{|A{F_1}|}}{d_1}=\frac{{|A{F_2}|}}{d_2}$;
(2)设A为椭圆上任一点,AF1,AF2分别与椭圆交于B,C两点,则$\frac{{|A{F_1}|}}{{|{F_1}B|}}+\frac{{|A{F_2}|}}{{|{F_2}C|}}≥\frac{{2(1+{e^2})}}{{1-{e^2}}}$(当且仅当点A在椭圆的顶点取等);
(3)设A为椭圆上且不在坐标轴上的任一点,过A的椭圆切线为l,M为线段F1F2上一点,且$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{{|{F_1}M|}}{{|M{F_2}|}}$,则直线AM⊥l;
(4)面积为2ab的椭圆内接四边形仅有1个.
其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)根据椭圆的第二定义可知$\frac{A{F}_{1}}{{d}_{2}}=\frac{A{F}_{2}}{{d}_{1}}=e$;
(2),分别取点A为椭圆的四个顶点验证,符合题意;
(3),由$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{{|{F_1}M|}}{{|M{F_2}|}}$,得AM为∠F1AF2的角平分线,得直线AM⊥l;
(4),当四边形的四个顶点为椭圆的定点时和分布在四个象限都可以.
解答 解:对于(1)根据椭圆的第二定义可知$\frac{A{F}_{1}}{{d}_{2}}=\frac{A{F}_{2}}{{d}_{1}}=e$,故错;
对于(2),分别取点A为椭圆的四个顶点验证,符合题意,故正确;
对于(3),A为椭圆上且不在坐标轴上的任一点,过A的椭圆切线为l,则∠F1AF2的角平分线垂直l,∵$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{{|{F_1}M|}}{{|M{F_2}|}}$,∴AM为∠F1AF2的角平分线,故正确;
对于(4),当四边形的四个顶点为椭圆的定点时和分布在四个象限都可以,故错.
故答案为:B.
点评 本题考查了椭圆的性质,比较难,但可以采用特殊情况验证法判定,属于压轴题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
9.在区间[-1,3]内任取一个实数x满足log2(x-1)>0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
10.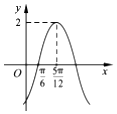 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | $f(x)=2sin({x-\frac{π}{6}})$ | B. | $f(x)=2sin({2x-\frac{π}{3}})$ | C. | $f(x)=2sin({x+\frac{π}{12}})$ | D. | $f(x)=2sin({2x-\frac{π}{6}})$ |
14. 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )| A. | 44,45,56 | B. | 44,43,57 | C. | 44,43,56 | D. | 45,43,57 |