题目内容
4.已知f(x)=asinx,g(x)=lnx,其中a∈R(y=g-1(x)与y=g(x)关于直线y=x对称)(1)若函数G(x)=f(1-x)+g(x)在区间(0,1)上递增,求a的取值范围;
(2)证明:$\sum_{k=1}^n{sin\frac{1}{{{{(1+k)}^2}}}<ln2}$;
(3)设F(x)=g-1(x)-mx2-2(x+1)+b(m<0),其中F(x)>0恒成立,求满足条件的最小整数b的值.
分析 (1)化简$G(x)=asin(1-x)+lnx,{G^/}(x)=\frac{1}{x}-acos(1-x)>0$恒成立,分离变量,利用函数的单调性推出结果即可.
(2)当a=1时,G(x)=sin(1-x)+lnx在(0,1)单调增,推出$sin\frac{1}{{{{(1+k)}^2}}}=sin[1-\frac{{{k^2}+2k}}{{{{(1+k)}^2}}}]<ln\frac{{{{(k+1)}^2}}}{{{k^2}+2k}}$
然后证明即可.
(3)化简F(x)=ex-mx2-2x+b-2>0即:F(x)min>0,求出导数F′(x)=ex-2mx-2,二次导数F∥(x)=ex-2m判断导函数的符号,推出函数的单调性,求出最值,列出不等式,$b>(\frac{x_0}{2}-1){e^{x_0}}+{x_0}+2$,x0∈(0,ln2)恒成立,构造函数,利用函数的导数,求解最值,然后推出最小整数b的值.
解答 解:(1)由题意:$G(x)=asin(1-x)+lnx,{G^/}(x)=\frac{1}{x}-acos(1-x)>0$恒成立,
则$a<\frac{1}{xcos(1-x)}$恒成立.又$y=\frac{1}{xcos(1-x)}$单调递减,∴a≤1
(2)由(1)知,当a=1时,G(x)=sin(1-x)+lnx在(0,1)单调增
∴sin(1-x)+lnx<G(1)=0∴$sin(1-x)<ln\frac{1}{x}(0<x<1)$
∴$sin\frac{1}{{{{(1+k)}^2}}}=sin[1-\frac{{{k^2}+2k}}{{{{(1+k)}^2}}}]<ln\frac{{{{(k+1)}^2}}}{{{k^2}+2k}}$
∴$\sum_{k=1}^{n}sin\frac{1}{(1+k)^{2}}<ln(\frac{{2}^{2}}{1×3}•\frac{{3}^{2}}{2×4}…\frac{{k}^{2}}{(k-1)(k+1)}•\frac{(k+1)^{2}}{k(k+2)})$=$\frac{k+1}{k+2}ln2<ln2$.
(3)由F(x)=g-1(x)-mx2-2(x+1)+b=ex-mx2-2x+b-2>0
即:F(x)min>0又F′(x)=ex-2mx-2,F′′(x)=ex-2m,
∵m<0
则F∥(x)>0,∴F′(x),单调增,又F′(0)<0,F′(1)>0
则必然存在x0∈(0,1),使得F′(x0)=0,
∴F(x)在(-∞,x0)单减,(x0,+∞)单增,
∴$F(x)≥F({x_0})={e^{x_0}}-m{x_0}^2-2{x_0}+b-2>0$
则$b>-{e^{x_0}}+m{x_0}^2+2{x_0}+2$,又${e^{x_0}}-2m{x_0}-2=0$∴$m=\frac{{{e^{x_0}}-2}}{{2{x_0}}}$
∴$b>-{e^{x_0}}+\frac{{{x_0}({e^{x_0}}-2)}}{2}+2{x_0}+2=(\frac{x_0}{2}-1){e^{x_0}}+{x_0}+2$
又m<0,则x0∈(0,ln2)
∴$b>(\frac{x_0}{2}-1){e^{x_0}}+{x_0}+2$,x0∈(0,ln2)恒成立
令m(x)=$(\frac{x}{2}-1){e^x}+x+2$,x∈(0,ln2)
则${m^/}(x)=\frac{1}{2}(x-1){e^x}+1$,m″(x)=$\frac{1}{2}x{e}^{x}>0$,
∴m′(x)在x∈(0,ln2)单调递增 又${m^/}(0)=\frac{1}{2}>0$
∴m′(x)>0∴m(x)在x∈(0,ln2)单调递增,
∴m(x)<m(ln2)=2ln2,∴b>2ln2又b为整数.
∴最小整数b的值为:2.
点评 本题考查函数的导数的综合应用,函数的单调性以及函数的最值的求法,二次导数的应用,考查构造法以及转化思想的应用,难度比较大.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案组对应数据如表所示:
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | a |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
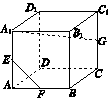 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | y=|x| | B. | y=-x3 | C. | y=($\frac{1}{2}$)x | D. | y=$\frac{1}{x}$ |
 如图所示,沿河有A、B两城镇,它们相距20千米,以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放,两城镇可以单独建污水处理厂,或者联合建污
如图所示,沿河有A、B两城镇,它们相距20千米,以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放,两城镇可以单独建污水处理厂,或者联合建污