题目内容
设点P是圆x2+(y+1)2=
上的动点,过点P作抛物线x2=4y的两条切线,切点为A、B,求
•
的最小值及取得最小值时P点的坐标.
| 3 |
| 4 |
| PA |
| PB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设出切线的方程,并与抛物线的方程联立,由相切可得△=0,利用根与系数的关系及数量积即可得出
•
,再利用点P在圆上及函数的导数即可求出最小值.
| PA |
| PB |
解答:
解:由题意可知:切线PA、PB的斜率都存在,分别为k1,k2,切点A(x1,y1),B(x2,y2).
设过点P的抛物线的切线l:y=k(x-m)+n,代入x2=4y,
可得x2-4kx+(4km-4n)=0(*).
∵直线l与抛物线相切,∴△=16k2-4×(4km-4n)=0,化为k2-km+n=0.
∴k1+k2=m,k1k2=n.(**)
此时,x1=2k1,y1=
=k12;同理,x2=2k2,y2=k22.
∴
•
=(x1-m)(x2-m)+(y1-n)(y2-n)
=(2k1-m)(2k2-m)+(k12-n)(k22-n)
=4k1k2-2m(k1+k2)+m2+(k1k2)2-n[(k1+k2)2-2k1k2]+n2
=4n-2m2+m2+n2-n(m2-2n)+n2
=4n2+4n-m2(1+n).
∵点P(m,n)在圆C1上,
∴m2+(n+1)2=
,即 m2=
-(n+1)2,
代入上式可得
•
=n3+7n2+
n+
,
考查函数f(n)═n3+7n2+
n+
(-1-
≤n≤-1+
),.
求得f′(n)=3n2+14n+
=
(2n+1)6n+25),
令f′(n)=0,解得n=-
,或 n=-
.
当n∈(-1-
-
)时,f′(n)<0,f(n)为减函数,
当n∈(-
,-1+
)时,f′(n)>0,f(n)为增函数,
故当n=-
f(n)取得最小值为f(-
)=-
,
此时对应的点P(±
,-
).
设过点P的抛物线的切线l:y=k(x-m)+n,代入x2=4y,
可得x2-4kx+(4km-4n)=0(*).
∵直线l与抛物线相切,∴△=16k2-4×(4km-4n)=0,化为k2-km+n=0.
∴k1+k2=m,k1k2=n.(**)
此时,x1=2k1,y1=
| x12 | ||
|
∴
| PA |
| PB |
=(2k1-m)(2k2-m)+(k12-n)(k22-n)
=4k1k2-2m(k1+k2)+m2+(k1k2)2-n[(k1+k2)2-2k1k2]+n2
=4n-2m2+m2+n2-n(m2-2n)+n2
=4n2+4n-m2(1+n).
∵点P(m,n)在圆C1上,
∴m2+(n+1)2=
| 3 |
| 4 |
| 3 |
| 4 |
代入上式可得
| PA |
| PB |
| 25 |
| 4 |
| 1 |
| 4 |
考查函数f(n)═n3+7n2+
| 25 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
求得f′(n)=3n2+14n+
| 25 |
| 4 |
| 1 |
| 4 |
令f′(n)=0,解得n=-
| 1 |
| 2 |
| 25 |
| 6 |
当n∈(-1-
| ||
| 2 |
| 1 |
| 2 |
当n∈(-
| 1 |
| 2 |
| ||
| 2 |
故当n=-
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
此时对应的点P(±
| ||
| 2 |
| 1 |
| 2 |
点评:熟练掌握圆锥曲线的定义与性质、直线与圆锥曲线相切问题的解决模式、根与系数的关系、利用导数求函数的最值等是解题的关键,属于中档题.

练习册系列答案
相关题目
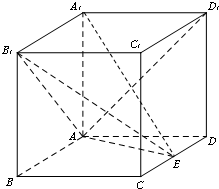 在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.
在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点. 根据如图所示的三视图画出对应的几何体.
根据如图所示的三视图画出对应的几何体.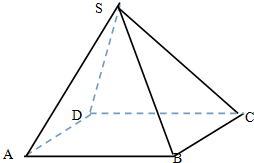 如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.
如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.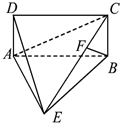 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.