题目内容
设f(x)=2x,g(x)=4x,且满足g[g(x)]>g[f(x)]>f[g(x)],求x的取值范围.
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:根据题意,求出g[g(x)]、g[f(x)]和f[g(x)]的表达式,
再利用指数函数、对数函数的性质化简不等式,从而求出x的取值范围.
再利用指数函数、对数函数的性质化简不等式,从而求出x的取值范围.
解答:
解:∵f(x)=2x,g(x)=4x,
∴g[g(x)]=g[4x]=44x,
g[f(x)]=g[2x]=42x,
f[g(x)]=f[4x]=24x;
又∵g[g(x)]>g[f(x)]>f[g(x)],
∴44x>42x>24x,
两边取对数,得
4x•lg4>2x•lg4>4x•lg2,
∴2•22x>2•2x>22x;
即22x+1>2x+1>22x,
∴2x+1>x+1>2x,
解得0<x<1;
∴x的取值范围是{x|0<x<1}.
∴g[g(x)]=g[4x]=44x,
g[f(x)]=g[2x]=42x,
f[g(x)]=f[4x]=24x;
又∵g[g(x)]>g[f(x)]>f[g(x)],
∴44x>42x>24x,
两边取对数,得
4x•lg4>2x•lg4>4x•lg2,
∴2•22x>2•2x>22x;
即22x+1>2x+1>22x,
∴2x+1>x+1>2x,
解得0<x<1;
∴x的取值范围是{x|0<x<1}.
点评:本题考查了指数函数与对数函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、函数的极大值大于函数的极小值 |
| B、若f′(x0)=0,则x0为函数f(x)的极值点 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
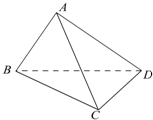 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形. 如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体.
如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体. 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.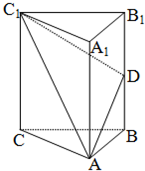 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,