题目内容
已知向量
=(sinx,cosx),
=(
,
),x∈R,函数f(x)=
.
(Ⅰ)求f(x)的最大值;
(Ⅱ)在△ABC中,设角A,B的对边分别为a,b,若B=2A,且b=2af(A-
),求角C的大小.
| m |
| n |
| 3 |
| 2 |
| ||
| 2 |
| m• |
| n |
(Ⅰ)求f(x)的最大值;
(Ⅱ)在△ABC中,设角A,B的对边分别为a,b,若B=2A,且b=2af(A-
| π |
| 6 |
考点:正弦定理,平面向量数量积的运算,余弦定理
专题:三角函数的求值
分析:(Ⅰ)由两向量的坐标,利用平面向量的数量积运算法则列出f(x)解析式,根据正弦函数的值域即可确定出f(x)的最大值;
(Ⅱ)根据第一问确定的f(x)解析式及正弦定理化简已知等式,由sinA不为0求出tanA的值,确定出A的度数,进而求出B的度数,即可确定出C的度数.
(Ⅱ)根据第一问确定的f(x)解析式及正弦定理化简已知等式,由sinA不为0求出tanA的值,确定出A的度数,进而求出B的度数,即可确定出C的度数.
解答:
解:(Ⅰ)f(x)=
•
=
sinx+
cosx=
sin(x+
),
∵-1≤sin(x+
)≤1,即-
≤
sin(x+
)≤
,
∴f(x)的最大值为
;
(Ⅱ)∵b=2af(A-
),
∴由(1)及正弦定理,化简得:sinB=2
sin2A,
又B=2A,∴sin2A=2
sin2A,
即2sinAcosA=
sin2A,
∵A是三角形的内角,∴sinA≠0,
∴cosA=
sinA,即tanA=
,
∴A=
,B=2A=
,
则C=π-(A+B)=
.
| m |
| n |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵-1≤sin(x+
| π |
| 6 |
| 3 |
| 3 |
| π |
| 6 |
| 3 |
∴f(x)的最大值为
| 3 |
(Ⅱ)∵b=2af(A-
| π |
| 6 |
∴由(1)及正弦定理,化简得:sinB=2
| 3 |
又B=2A,∴sin2A=2
| 3 |
即2sinAcosA=
| 3 |
∵A是三角形的内角,∴sinA≠0,
∴cosA=
| 3 |
| ||
| 3 |
∴A=
| π |
| 6 |
| π |
| 3 |
则C=π-(A+B)=
| π |
| 2 |
点评:此题考查了正弦定理,平面向量的数量积运算,正弦函数的值域,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
在5×5的棋盘中,放入3颗黑子和2颗白子,它们均不在同一行且不在同一列,则不同的排列方法种数为( )
| A、150 | B、200 |
| C、600 | D、1200 |
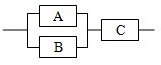 某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为
某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为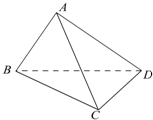 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.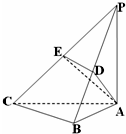 已知三棱锥P-ABC,∠PAC=∠ABC=90°,PA=AC=2BC,平面PAC⊥平面ABC,D、E分别是PB、PC的中点.
已知三棱锥P-ABC,∠PAC=∠ABC=90°,PA=AC=2BC,平面PAC⊥平面ABC,D、E分别是PB、PC的中点. 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.