题目内容
设点P(a,b)抛物线y=-2x2上任一点,则
-b的最小值为 .
| (a-3)2+(b+1)2 |
考点:函数的最值及其几何意义
专题:计算题,数形结合
分析:求出抛物线的焦点坐标与准线方程,根据两点间距离公式与抛物线的定义得
-b=|PA|+dP-x轴=
-b=|PA|+|PF|-
,利用|PF|+|PA|≥|FA|求得最小值.
| (a-3)2+(b+1)2 |
| (a-3)2+(b+1)2 |
| 1 |
| 8 |
解答:
解:由抛物线y=-2x2方程得其焦点F(0,-
),准线方程为y=
,
∵y=-2x2≤0,∴b≤0,
设A(3,-1),
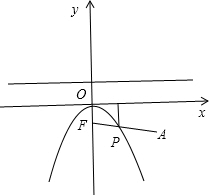
∴
-b=|PA|+dP-x轴
根据抛物线的定义,dP-x轴=|PF|-
,
∴
-b=|PA|+|PF|-
≥|AF|-
=
-
=3.
故答案为:3
| 1 |
| 8 |
| 1 |
| 8 |
∵y=-2x2≤0,∴b≤0,
设A(3,-1),

∴
| (a-3)2+(b+1)2 |
根据抛物线的定义,dP-x轴=|PF|-
| 1 |
| 8 |
∴
| (a-3)2+(b+1)2 |
| 1 |
| 8 |
≥|AF|-
| 1 |
| 8 |
| 25 |
| 8 |
| 1 |
| 8 |
故答案为:3
点评:本题考查了函数的最值的求法,考查了抛物线的定义,利用数形结合思想将代数式转化为几何中线段的长度是解答本题的关键,运算要细心.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知⊙M经过双曲线S:
-
=1的一个顶点和一个焦点,圆心M在双曲线上S上,则圆心M到双曲线S的中心的距离为( )
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
| A、一个命题的逆命题为真,则它的逆否命题一定为真 |
| B、若a+b>3,则a>1或b>2 |
| C、命题“所有的矩形都是正方形”的否命题和命题的否定均为真命题 |
| D、“a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
在5×5的棋盘中,放入3颗黑子和2颗白子,它们均不在同一行且不在同一列,则不同的排列方法种数为( )
| A、150 | B、200 |
| C、600 | D、1200 |
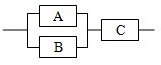 某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为
某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为