题目内容
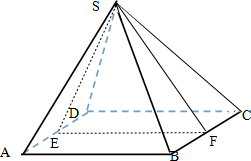
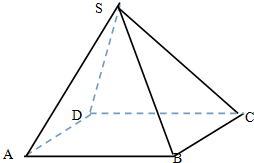如图四棱锥S-ABCD中，底面是边长为2厘米的正方形，侧棱长都是2厘米．（1）画出该棱锥的三视图，并标明尺寸；
（2）求该棱锥中二面角A-SB-C的大小的余弦值．
考点：与二面角有关的立体几何综合题,简单空间图形的三视图
专题：计算题,空间位置关系与距离,空间角
分析：（1）正视图与过P且与底面垂直的截面完全相同．
（2）利用正视图顶角，就是面ASD与面BSC所成二面角的大小，利用余弦定理求出结果即可．
（2）利用正视图顶角，就是面ASD与面BSC所成二面角的大小，利用余弦定理求出结果即可．
解答：
解：
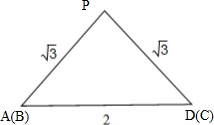
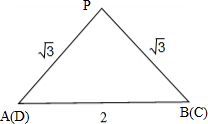
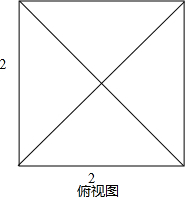
（1）（如图）几何体的三视图，正视图中，PA与PD重合为PE，（E为AD是中点，PE⊥AD，PE=
），
PB与PC重合为PF，（F是BC的中点，并且PF⊥BC，PF=
）．
∵几何体是正四棱锥，
∴侧视图与正视图相同．…（6分
（等腰三角形（3分），底边长（1分），腰长2分）
（2）四棱锥S-ABCD中，底面是边长为2厘米的正方形，侧棱长都是2厘米，
由（1）正视图可知，平面ASD与平面BSC所成角就是正视图中∠APB，
∴面ASD与面BSC所成二面角的大小的余弦值为：cos∠APB=
=
．
解：（1）（如图）几何体的三视图，正视图中，PA与PD重合为PE，（E为AD是中点，PE⊥AD，PE=
| 3 |
PB与PC重合为PF，（F是BC的中点，并且PF⊥BC，PF=
| 3 |
∵几何体是正四棱锥，
∴侧视图与正视图相同．…（6分
（等腰三角形（3分），底边长（1分），腰长2分）
（2）四棱锥S-ABCD中，底面是边长为2厘米的正方形，侧棱长都是2厘米，
由（1）正视图可知，平面ASD与平面BSC所成角就是正视图中∠APB，
∴面ASD与面BSC所成二面角的大小的余弦值为：cos∠APB=
(
| ||||
2×
|
| 1 |
| 3 |
点评：本题考查异面直线所成角的大小的求解和二面角的求法，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．
练习册系列答案
名校课堂系列答案
相关题目
下列说法正确的是（ ）
| A、一个命题的逆命题为真，则它的逆否命题一定为真 |
| B、若a+b＞3，则a＞1或b＞2 |
| C、命题“所有的矩形都是正方形”的否命题和命题的否定均为真命题 |
| D、“a2+b2=0，则a，b全为0”的逆否命题是“若a，b全不为0，则a2+b2≠0” |
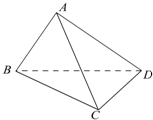在四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．
如图，在直三棱柱ABC-A1B1C1中，AA1=AB=BC=3，AC=2，D是AC的中点．
已知斜三棱柱ABC-A1B1C1，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．