题目内容
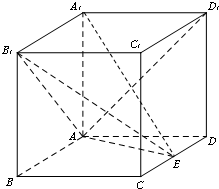 在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.
在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.(1)求直线B1E与直线AD1所成的角的余弦值;
(2)若AB=2,求二面角A-B1E-
| A | _ |
(3)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.
考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)由题意及所给的图形,分别以AB,AD,AA1为x轴、y轴、z轴建立空间直角坐标系,设AB=a,给出图形中各点的坐标,可求出向量
、
的坐标,验证其数量积为0即可得出结论;
(2)由题设条件,可求夹二面角的两个平面的法向量,可得两平面的夹角的余弦,即可求二面角A-B1E-
1的大小;
(3)由题意,可先假设在棱AA1上存在一点P(0,0,z0),使得DP∥平面B1AE,求出平面B1AE法向量,利用法向量与直线DP的方向向量数量积为0,由此方程解出z0的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.
| AD1 |
| B1E |
(2)由题设条件,可求夹二面角的两个平面的法向量,可得两平面的夹角的余弦,即可求二面角A-B1E-
| A | _ |
(3)由题意,可先假设在棱AA1上存在一点P(0,0,z0),使得DP∥平面B1AE,求出平面B1AE法向量,利用法向量与直线DP的方向向量数量积为0,由此方程解出z0的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.
解答:
解:(1)分别以AB,AD,AA1为x轴、y轴、z轴建立空间直角坐标系,设AB=a则A(0,0,0),D(0,1,0),D1(0,1,1),E(
,1,0),B1(a,0,1),
∴
=(0,1,1),
=(-
,1,-1),
=(a,0,1),
=(
,1,0),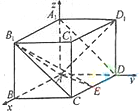
∵
•
=1-1=0
∴B1E⊥AD1,
∴直线B1E与直线AD1所成的角的余弦值为0;
(2)连接A1D,B1C,由长方体ABCD-A1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,∴AD1⊥B1C.
由(1)知,B1E⊥AD1,且B1C∩B1E=B1.
∴AD1⊥平面DCB1A1,
∴
是平面A1B1E的一个法向量,此时
=(0,1,1)
AB=2,设平面B1AE的法向量
=(x,y,z),则
=(2,0,1),
=(1,1,0)
∵
⊥平面B1AE,∴
⊥
,
⊥
,
得
取x=1,使得平面B1AE的一个法向量
=(1,-1,2),
设
与
所成的角为θ,则
cosθ=
=-
∴二面角A-B1E-A1的大小为30°;
(3)假设在棱AA1上存在一点P(0,0,z0)使得DP∥平面B1AE.此时
=(0,-1,z0)
又设AB的长度为a,平面B1AE的法向量
=(x,y,z),则
=(a,0,1),
=(
,1,0)
∵
⊥平面B1AE∴
⊥
,
⊥
得
取x=1,使得平面B1AE的一个法向量
=(1,
,-a)
要使DP∥平面B1AE,只要
⊥
,有
-az0=0,解得z0=
又DP?平面B1AE,∴存在点P,满足DP∥平面B1AE,此时AP=
.
| a |
| 2 |
∴
| AD1 |
| B1E |
| a |
| 2 |
| AB1 |
| AE |
| a |
| 2 |

∵
| AD1 |
| B1E |
∴B1E⊥AD1,
∴直线B1E与直线AD1所成的角的余弦值为0;
(2)连接A1D,B1C,由长方体ABCD-A1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,∴AD1⊥B1C.
由(1)知,B1E⊥AD1,且B1C∩B1E=B1.
∴AD1⊥平面DCB1A1,
∴
| AD1 |
| AD1 |
AB=2,设平面B1AE的法向量
| n |
| AB1 |
| AE |
∵
| n |
| n |
| AB1 |
| n |
| AE |
得
|
取x=1,使得平面B1AE的一个法向量
| n |
设
| AD1 |
| n |
cosθ=
| ||||
|
|
| ||
| 2 |
∴二面角A-B1E-A1的大小为30°;
(3)假设在棱AA1上存在一点P(0,0,z0)使得DP∥平面B1AE.此时
| DP |
又设AB的长度为a,平面B1AE的法向量
| n |
| AB1 |
| AE |
| a |
| 2 |
∵
| n |
| n |
| AB1 |
| n |
| AE |
|
取x=1,使得平面B1AE的一个法向量
| n |
| -a |
| 2 |
要使DP∥平面B1AE,只要
| n |
| DP |
| a |
| 2 |
| 1 |
| 2 |
又DP?平面B1AE,∴存在点P,满足DP∥平面B1AE,此时AP=
| 1 |
| 2 |
点评:本题考查利用空间向量这一工具求二面角,证明线面平行,解题的关键是建立恰当的坐标系及空间位置关系与向量的对应.

练习册系列答案
相关题目
下列说法正确的是( )
| A、一个命题的逆命题为真,则它的逆否命题一定为真 |
| B、若a+b>3,则a>1或b>2 |
| C、命题“所有的矩形都是正方形”的否命题和命题的否定均为真命题 |
| D、“a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
在5×5的棋盘中,放入3颗黑子和2颗白子,它们均不在同一行且不在同一列,则不同的排列方法种数为( )
| A、150 | B、200 |
| C、600 | D、1200 |
下列说法正确的是( )
| A、函数的极大值大于函数的极小值 |
| B、若f′(x0)=0,则x0为函数f(x)的极值点 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
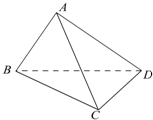 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.