题目内容
下列函数在区间(-1,1)上单调递增的是( )
A、y=
| ||
| B、y=x2 | ||
| C、y=x3 | ||
| D、y=lnx |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:结合反比例函数,二次函数,三次函数,对数函数的单调性,分析四个答案中函数在区间(-1,1)上的单调性,可得答案.
解答:
解:A中,x=0时,函数y=
无意义,故函数在区间(-1,0)和(0,1)上均为减函数,但在(-1,1)上不具单调性,不满足要求;
B中,y=x2在区间(-1,0]为减函数,在[0,1)上为增函数,但在(-1,1)上不具单调性,不满足要求;
C中,y=x3在(-1,1)上单调递增,满足要求;
D中,当x∈(-1,0]时,函数y=lnx无意义,不满足要求;
故选:C
| 1 |
| x |
B中,y=x2在区间(-1,0]为减函数,在[0,1)上为增函数,但在(-1,1)上不具单调性,不满足要求;
C中,y=x3在(-1,1)上单调递增,满足要求;
D中,当x∈(-1,0]时,函数y=lnx无意义,不满足要求;
故选:C
点评:本题考查复合函数的单调性、反比例函数,二次函数,三次函数,对数函数及一次函数的性质,属中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
椭圆
+
=1的焦点坐标是( )
| x2 |
| 25 |
| y2 |
| 169 |
| A、(±5,0) |
| B、(0,±5) |
| C、(0,±12) |
| D、(±12,0) |
根据如图所示各图中三角形的个数,推断第10个图中三角形的个数是( )


| A、60 | B、62 | C、65 | D、66 |
用火柴棒摆“金鱼”,如图所示,按照如图的规律,第4个“金鱼”图需要火柴棒的根数为( )


| A、24 | B、26 | C、28 | D、30 |
根据下列条件解三角形,两解的是( )
| A、b=10,A=45°,B=70° |
| B、a=60,c=48,B=100° |
| C、a=14,b=16,A=45° |
| D、a=7,b=5,A=80° |
已知a,b为正实数且ab=1,若不等式(x+y)(
+
)>M对任意正实数x,y恒成立,则实数M的取值范围是( )
| a |
| x |
| b |
| y |
| A、[4,+∞) |
| B、(-∞,1] |
| C、(-∞,4] |
| D、(-∞,4) |
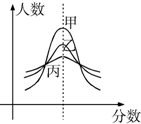 某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中正确的是( )
某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中正确的是( )| A、甲学科总体的方差最小 |
| B、丙学科总体的均值最小 |
| C、乙学科总体的方差及均值都居中 |
| D、甲、乙、丙的总体的均值不相同 |