题目内容

根据如图所示各图中三角形的个数，推断第10个图中三角形的个数是（　　）
A、60B、62C、65D、66
考点：归纳推理
专题：规律型
分析：本题考查的知识点是归纳推理，方法是根据已知图形编号与三角形个数的关系，然后总结归纳其中的规律，写出其通项，将n=10代入可得答案．
解答： 解：第1个图中，共有1+2=3个三角形；
第2个图中，共有1+2+3=6个三角形；
第3个图中，共有1+2+3+4=10个三角形；
第4个图中，共有1+2+3+4+5=15个三角形；
第5个图中，共有1+2+3+4+5+6=21个三角形；
…
由此归纳可得：
第n个图中，共有1+2+3+4+…+n+（n+1）=
(1+n+1)(n+1)
2
=
(n+1)(n+2)
2
个三角形；
当n=10时，
(n+1)(n+2)
2
=
11×12
2
=66，
故第10个图中三角形的个数是66个，
故选：D
点评：归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
相关题目
已知定义在R上的函数y=f（x）对任意的x都满足f（x+1）=-f（x），当-1≤x＜1时，f（x）=x2，函数g（x）=
log3(x-1)(x＞1)
2x(x≤1)
，则函数h（x）=f（x）-g（x）在区间[-5，5]内的零点个数为
 
．
在平面直角坐标系中，若向量
a
=（x1，y1），
b
=（x2，y2）且
a
⊥
b
，则x1x2+y1y2=0．把上述结论类比推广到空间：在空间直角坐标系中，若向量
a
=（x1，y1，z1），
b
=（x2，y2，z2），且
a
⊥
b
，则
 
．
已知正实数x，y满足（x-1）（y+1）=4，则x+y的最小值为
 
．
下列四个函数中，在（0，+∞）上是减函数的是（　　）
A、f（x）=x+3
B、f（x）=（x-1）2
C、f（x）=
1
x
+1
D、f（x）=|x|
下列函数在区间（-1，1）上单调递增的是（　　）
A、y=
1
x
B、y=x2
C、y=x3
D、y=lnx
已知数列{an}的前n项和为Sn=n2-5n+2，则数列{|an|}的前10项和为（　　）
A、56B、58C、62D、60
在△ABC中的内角A，B，C所对的边分别为a，b，c，若∠B=60°，a，b，c成等比数列，则△ABC的形状为（　　）
A、直角三角形B、等腰三角形
C、等边三角形D、不确定
如图是导函数y=f′（x）的图象，那么函数y=f（x）在下面哪个区间是减函数（　　）
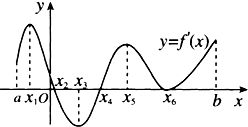
A、（x1，x3）
B、（x2，x4）
C、（x4，x6）
D、（x5，x6）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网