题目内容
20.已知曲线f(x)=ax-1+1(a>1)恒过定点A,点A恰在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线上,则双曲线C的离心率为( )| A. | $\sqrt{5}$ | B. | 5 | C. | 2 | D. | 2$\sqrt{2}$ |
分析 求出A的坐标,利用点A恰在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线上,得出$\frac{b}{a}$=2,即可求出双曲线C的离心率.
解答 解:曲线f(x)=ax-1+1(a>1)恒过定点A(1,2),
∵点A恰在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线上,
∴$\frac{b}{a}$=2,
∴b=2a,c=$\sqrt{5}$a,
∴e=$\frac{c}{a}$=$\sqrt{5}$,
故选A.
点评 本题考查函数过定点,考查双曲线的方程与性质,确定A的坐标是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
8.已知等边三角形的边长为1,那么它的平面直观图面积为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{8}$ | C. | $\frac{\sqrt{6}}{8}$ | D. | $\frac{\sqrt{6}}{16}$ |
15.如图所示,某人拨通了电话,准备手机充值须如下操作( )
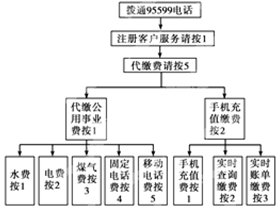

| A. | 1511 | B. | 1515 | C. | 1521 | D. | 1523 |
12.已知集合A={x|(x-2)(x+3)<0},B={x|y=$\sqrt{\frac{1}{x+1}}$},则A∩(∁RB)=( )
| A. | [-3,-1] | B. | (-3,-1] | C. | (-3,-1) | D. | [-1,2] |
10.已知0<c<1,a>b>1,下列不等式成立的是( )
| A. | ca>cb | B. | ac<bc | C. | $\frac{a}{a-c}>\frac{b}{b-c}$ | D. | logac>logbc |
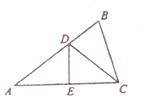 如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.
如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.