题目内容
 如图所示,菱形ABCD的边长为
如图所示,菱形ABCD的边长为| 3 |
| BP |
| PA |
| PC |
| BP |
| PA |
| PC |
考点:向量在几何中的应用
专题:平面向量及应用
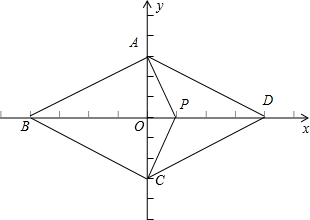
分析:利用菱形的几何性质可知,线段BP所在直线与AC垂直,再结合减法几何意义,容易得第(1)结果为0;第(2)问涉及到了范围的计算问题,又菱形具有建系的充分条件,因此利用建系把问题变成坐标运算问题,最终转化为函数的值域问题.
解答:
解:∵菱形ABCD,∴对角线CA⊥BD,又
-
=
,且点P为对角线BD上任意一点,
∴
∥
∴
⊥
,∴
•
=0,∴
•(
-
)=0;
对于第二问:
如图建立坐标系,∵菱形ABCD的边长为
,∠ABC=60°∴∠ADO=30°,∴|
|=
cos30°=
,|
|=
sin30°=
,
∴B(-
,0),D(
,0),设P(x,0)则由已知得 -
≤x≤
,由菱形的性质,
+
=2
=(-2x,0),而
=(x+
,0),
∴
•(
+
)=
•2
=(x+
,0)•(-2x,0)=-2x2-3x=-2(x+
)2+
,
又∵-
≤x≤
,该函数在[-
,-
]上递增,在(-
,
]上递减,
所以当x=
时,取得最小值-9;当x=-
时,取得最大值
,所以所求的取值范围是[-9,
].
故答案为0,[-9,
]
| PA |
| PC |
| CA |
∴
| BP |
| BD |
| BP |
| CA |
| BP |
| CA |
| BP |
| PA |
| PC |
对于第二问:
如图建立坐标系,∵菱形ABCD的边长为
| 3 |
| OD |
| 3 |
| 3 |
| 2 |
| OA |
| 3 |
| ||
| 2 |
∴B(-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| PA |
| PC |
| PO |
| BP |
| 3 |
| 2 |
∴
| BP |
| PA |
| PC |
| BP |
| PO |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 8 |
又∵-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
所以当x=
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 8 |
| 9 |
| 8 |
故答案为0,[-9,
| 9 |
| 8 |

点评:将菱形的几何性质和向量加法、减法、数乘及内积运算的几何意义结合起来,才能有效的解决问题.这个题建系后要注意引入的变量x的范围.

练习册系列答案
相关题目
已知数列{an}满足a1=1,a2=2,an+2=(1+cos2
)an+sin2
,则该数列的前18项和为( )
| nπ |
| 2 |
| nπ |
| 2 |
| A、2101 | B、2012 |
| C、1012 | D、1067 |