题目内容
13.甲、乙两企业根据赛事组委会要求为获奖者定做某工艺品作为奖品,其中一等奖奖品3件,二等奖奖品6件;制作一等奖、二等奖所用原料完全相同,但工艺不同,故价格有所差异.甲厂收费便宜,但原料有限,最多只能制作4件奖品,乙厂原料充足,但收费较贵,其具体收费如表所示,则组委会定做该工艺品的费用总和最低为4900元.| 奖品 缴费(无/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
分析 设甲生产一等奖奖品x,二等奖奖品为y,建立约束条件和目标函数,利用线性规划的知识进行求解.
解答 解:设甲生产一等奖奖品x,二等奖奖品为y,x,y∈N
则乙生产一等奖奖品3-x,二等奖奖品为6-y,
则满足$\left\{\begin{array}{l}{x+y≤4}\\{3-x≥0}\\{6-y≥0}\\{x,y≥0}\end{array}\right.$,
设费用为z,则z=500x+400y+800(3-x)+600(6-y)=-300x-200y+6000,
作出不等式组对应的平面区域如图:
平移z=-300x-200y+6000,
由图象知当直线经过点A时,直线截距最大,此时z最小,
由$\left\{\begin{array}{l}{x=3}\\{x+y=4}\end{array}\right.$,解得A(3,1),
组委会定做该工艺品的费用总和最低为z=-300×3-200+6000
=4900,
故生产一等奖奖品3个,二等奖奖品为1,其余都由乙生产,所用费用最低.
故答案为:4900.
点评 本题主要考查线性规划的应用,建立条件,利用数形结合是解决本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
3.已知抛物线C:y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合,则抛物线C的方程是( )
| A. | y2=2x | B. | y2=-2x | C. | y2=4x | D. | y2=-4x |
1.执行如图所示的程序框图,如果输出T=6,那么判断框内应填入的条件是( )
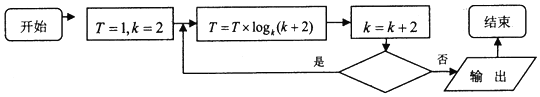
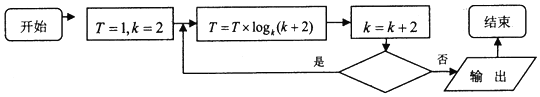
| A. | k<32 | B. | k<33 | C. | k<64 | D. | k<65 |
8.某公司的班车分别在7:30,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过15分钟的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{8}$ |
18.在如图所示的程序图中,若函数f(x)=$\left\{\begin{array}{l}{{2}^{x},αx≤0}\\{lo{g}_{\frac{1}{2}}x,x>0}\end{array}\right.$,则输出的结果是( )
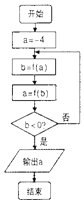

| A. | -3 | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
2.某公司安排6位员工在“元旦(1月1日至1月3日)”假期值班,每天安排2人,每人值班1天,则6位员工中甲不在1日值班的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
14.已知双曲线C与双曲线$\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{48}$=1有相同的渐近线,且与椭圆$\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{169}$=1有相同的焦点,则双曲线C的方程为( )
| A. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |