题目内容
3．已知抛物线C：y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合，则抛物线C的方程是（ ）| A． | y2=2x | B． | y2=-2x | C． | y2=4x | D． | y2=-4x |
分析 求出圆的圆心坐标，然后求解抛物线方程．
解答 解：圆x2+y2-2x-15=0的圆心（1，0），抛物线C：y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合，
可得：p=2，所求抛物线方程为：y2=4x．
故选：C．
点评 本题考查圆的方程的应用以及抛物线方程的求法，考查转化思想以及计算能力．
练习册系列答案
名题金卷系列答案
相关题目
13．我国古代有着辉煌的数学研究成果．《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经10部专著，有着十分丰富多彩的内容，是了解我国古代数学的重要文献．这10部专著中有7部产生于魏晋南北朝时期．某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容，则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为（ ）
| A． | $\frac{14}{15}$ | B． | $\frac{13}{15}$ | C． | $\frac{2}{9}$ | D． | $\frac{7}{9}$ |
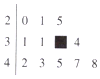在如图所示一组数据的茎叶图中，有一个数字被污染后而模糊不清，但曾计算得该组数据的极差与中位数之和为61，则被污染的数字为（ ）
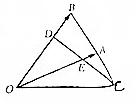在△ABO中，点C是点B关于点A的对称点，点D是OB靠近B的三等分点，DC与OA交于E点，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{OC}$，$\overrightarrow{CD}$．
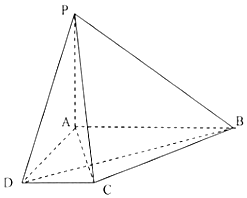如图，四棱锥P-ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，AP=AD=2CD=1，AB=2，PA⊥平面ABCD．
如图1为正方形ABCD的边长为2，AC∩BD=O，将正方形ABCD沿对角线BD折起，使AC=a，得到三棱锥A-BCD（如图2）