题目内容
4．对于函数g（x）=$\left\{\begin{array}{l}{sinπx，x∈（2，+∞）}\\{2g（x+2），x∈（0，2]}\end{array}\right.$，若关于x的方程g（x）=n（n＞0）有且只有两个不同的实根x1，x2，则x1+x2=1．分析 作出g（x）的函数图象，根据函数图象的对称性得出x1+x2．
解答 解：作出函数y=g（x）的图象如图所示：
∵关于x的方程g（x）=n（n＞0）有且只有两个不同的实根x1，x2，
∴x1，x2关于直线x=$\frac{1}{2}$对称，
∴x1+x2=1．
故答案为1．
点评 本题考查了函数零点的个数判断，三角函数的图象，属于中档题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
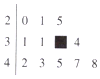在如图所示一组数据的茎叶图中，有一个数字被污染后而模糊不清，但曾计算得该组数据的极差与中位数之和为61，则被污染的数字为（ ）
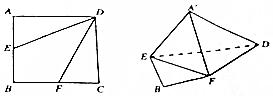如图，在边长为4的正方形ABCD中，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．