题目内容
 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于C,D,其中∠APE=30°.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于C,D,其中∠APE=30°.(1)求证:
| ED |
| BD |
| PB |
| PA |
| PD |
| PC |
(2)求∠PCE的大小.
考点:与圆有关的比例线段,平行线分线段成比例定理,弦切角
专题:直线与圆
分析:(1)由题意可知,∠EPC=∠APC,∠PEB=∠PAC,从而△PED∽△PAC,由此能证明
•
=
.
(2)由∠EPC=∠APC,∠PEB=∠PAC,得∠CDE=∠ECD,由此能求出∠PCE的大小.
| ED |
| BD |
| PB |
| PA |
| PD |
| PC |
(2)由∠EPC=∠APC,∠PEB=∠PAC,得∠CDE=∠ECD,由此能求出∠PCE的大小.
解答:
(本小题满分10分)
(1)证明:由题意可知,∠EPC=∠APC,∠PEB=∠PAC,
则△PED∽△PAC,则
=
,
又
=
,则
•
=
.(5分)
(2)解:由∠EPC=∠APC,∠PEB=∠PAC,
得∠CDE=∠ECD,
在△ECD中,∠CED=30°,
∴∠PCE=75°.(10分)
(1)证明:由题意可知,∠EPC=∠APC,∠PEB=∠PAC,
则△PED∽△PAC,则
| PE |
| PA |
| PD |
| PC |
又
| PE |
| PB |
| ED |
| BD |
| ED |
| BD |
| PB |
| PA |
| PD |
| PC |
(2)解:由∠EPC=∠APC,∠PEB=∠PAC,
得∠CDE=∠ECD,
在△ECD中,∠CED=30°,
∴∠PCE=75°.(10分)
点评:本小题主要考查平面几何的证明,具体涉及到弦切角定理以及三角形相似等内容.本小题重点考查考生对平面几何推理能力.

练习册系列答案
相关题目
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(23)+f(-14)=( )
| A、-1 | B、1 | C、-2 | D、2 |
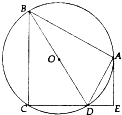 如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.
如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.