题目内容
若f（x）是R上周期为5的奇函数，且满足f（1）=1，f（2）=2，则f（23）+f（-14）=（ ）
| A、-1 | B、1 | C、-2 | D、2 |
考点：函数的周期性,函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性和周期性进行转化求解即可．
解答：
解：∵f（x）是R上周期为5的奇函数，且满足f（1）=1，f（2）=2，
∴f（23）+f（-14）=f（25-2）+f（-15+1）=f（-2）+f（1）
=-f（2）+f（1）=-2+1=-1，
故选：A
∴f（23）+f（-14）=f（25-2）+f（-15+1）=f（-2）+f（1）
=-f（2）+f（1）=-2+1=-1，
故选：A
点评：本题主要考查函数值的计算，根据函数奇偶性和周期性之间的关系进行转化是解决本题的关键．
练习册系列答案
相关题目
如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE，BE，∠APE的平分线与AE，BE分别交于C，D，其中∠APE=30°．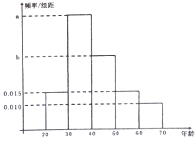
根据某电子商务平台的调查统计显示，参与调查的1000为上网购物者的年龄情况如图所示：