题目内容
7.已知定义在R上的函数f(x)满足f(x)•f(x+2)=13,则f(x)的一个周期为4.分析 利用题中条件:“f(x)•f(x+2)=13”得出f(x+4)=f(x),结合函数周期性的定义可知函数f(x)是周期函数.
解答 解:∵f(x)•f(x+2)=13
∴f(x+2)•f(x+4)=13,
∴f(x+4)=f(x),
∴f(x)是一个周期为4的周期函数,
故答案为:4.
点评 本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题.函数的周期性是高考函数题的重点考查内容,几个重要的周期公式要熟悉,如:(1)f(x+a)=f(x-a),则T=2a;(2)f(x+a)=-$\frac{1}{f(x)}$,则T=2a等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.若a=2x,b=$\sqrt{x}$,c=log${\;}_{\frac{1}{2}}$x,则“x>1”是“a>b>c”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
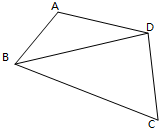 如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.
如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.