题目内容
19．关于x的一元二次方程3x2-5ax+2a=0的两个根x1和x2分别满足0＜x1＜1，x2＞2，求a的取值范围．分析 设f（x）=3x2-5ax+2a，则由题意可得$\left\{\begin{array}{l}{f（0）=2a＞0}\\{f（1）=3-3a＜0}\\{f（2）=12-8a＜0}\end{array}\right.$，由此求得a的范围．
解答 解：设f（x）=3x2-5ax+2a，则由题意可得$\left\{\begin{array}{l}{f（0）=2a＞0}\\{f（1）=3-3a＜0}\\{f（2）=12-8a＜0}\end{array}\right.$，求得a＞$\frac{3}{2}$．
点评 本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
9．连续抛掷骰子，记下每次面朝上的点数，若出现三个不同的数就停止，问抛掷5次停止时，会出现不同的结果种数位 （ ）
| A． | 420 | B． | 840 | C． | 720 | D． | 640 |
10．已知地球半径为R，地球上某地A的纬度是北纬60°，某同步卫星在赤道上空6R的轨道上，它每24小时绕地球一周，所以它定位于赤道上某一点B的上空C处，如果点B与点A在同一子午线上，在A第观察此卫星的仰角为α，那么sinα的值为（ ）
| A． | $\frac{5\sqrt{43}}{86}$ | B． | $\frac{\sqrt{21}}{21}$ | C． | $\frac{3\sqrt{21}}{21}$ | D． | $\frac{3\sqrt{21}}{42}$ |
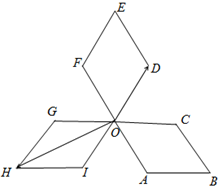如图，四边形OABC，ODEF，OGHI是三个全等的菱形，∠COD=∠FOG=∠AOI=60°，P为各菱形边上的动点，设$\overrightarrow{OP}=x\overrightarrow{OD}+y\overrightarrow{OH}$，则x+y的最大值为4．