题目内容
15．
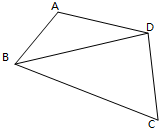如图，在四边形ABCD中，BC=6，AD=CD=4，∠A+∠C=π，记△BCD，△ABD的面积分别为S1，S2，求S1-S2的最大值．
分析 在△ABD，△BCD中，利用余弦定理表示BD，可得AB，即可求S1-S2的最大值．
解答 解：依题意可知，∠A+∠C=π，即∠A=π-∠C，设AB=x，则：
在△ABD中，由余弦定理得：BD2=x2+42-2×x×4cosA=x2+16-8xcosA，
在△BCD中，由余弦定理得：BD2=62+42-2×6×4cosC=52-48cosC=52+48cosA，
由x2+16-8xcosA=52+48cosA，
∴x=6-8cosA，
∴S1-S2=$\frac{1}{2}•4•6$sinC-$\frac{1}{2}$x•4sinA=16sinAcosA=8sin2A，
∴S1-S2的最大值是8．
点评 本题考查余弦定理的运用，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
6．已知f（x）=|xex|，方程f2（x）+tf（x）+1=0（t∈R）有四个实数根，则t的取值范围为（ ）
| A． | （$\frac{{e}^{2}+1}{e}$，+∞） | B． | （-∞，-$\frac{{e}^{2}+1}{e}$） | C． | （-$\frac{{e}^{2}+1}{e}$，-2） | D． | （2，$\frac{{e}^{2}+1}{e}$） |
10．已知地球半径为R，地球上某地A的纬度是北纬60°，某同步卫星在赤道上空6R的轨道上，它每24小时绕地球一周，所以它定位于赤道上某一点B的上空C处，如果点B与点A在同一子午线上，在A第观察此卫星的仰角为α，那么sinα的值为（ ）
| A． | $\frac{5\sqrt{43}}{86}$ | B． | $\frac{\sqrt{21}}{21}$ | C． | $\frac{3\sqrt{21}}{21}$ | D． | $\frac{3\sqrt{21}}{42}$ |
20．已知空间四边形OABC，点M在线段OA上，且OM=2MA，点N为BC的中点，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则$\overrightarrow{MN}$=（ ）
| A． | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{2}{3}$$\overrightarrow c$ | B． | -$\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | C． | $\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | D． | $\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}$$\overrightarrow c$ |