题目内容
16．若a=2x，b=$\sqrt{x}$，c=log${\;}_{\frac{1}{2}}$x，则“x＞1”是“a＞b＞c”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
分析 先画出函数的图象，根据图象以及充分条件，必要条件的定义即可判断a＞b＞c与x＞1的关系．
解答 解：画出函数y=a=2x，y=b=$\sqrt{x}$，y=c=log${\;}_{\frac{1}{2}}$x的图象，如图示：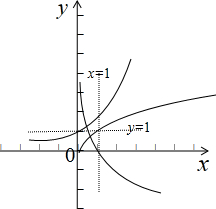
，
由图象得：x＞1时：a＞b＞c，是充分条件，
而a＞b＞c时，存在x＜1，即推不出x＞1，不是必要条件，
故选：A．
点评 本题考查指数函数、对数函数、幂函数的图象，充分条件，必要条件，必要不充分条件的概念．
练习册系列答案
高效智能课时作业系列答案
相关题目
6．已知f（x）=|xex|，方程f2（x）+tf（x）+1=0（t∈R）有四个实数根，则t的取值范围为（ ）
| A． | （$\frac{{e}^{2}+1}{e}$，+∞） | B． | （-∞，-$\frac{{e}^{2}+1}{e}$） | C． | （-$\frac{{e}^{2}+1}{e}$，-2） | D． | （2，$\frac{{e}^{2}+1}{e}$） |
1．已知函数y=f（x）是R上的偶函数，且在（-∞，0]上是减函数，若f（a）≥f（2），则实数a的取值范围是（ ）
| A． | （-∞，2] | B． | （-∞，-2]∪[2，+∞） | C． | [-2，+∞） | D． | [-2，2] |
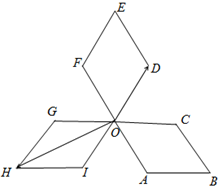如图，四边形OABC，ODEF，OGHI是三个全等的菱形，∠COD=∠FOG=∠AOI=60°，P为各菱形边上的动点，设$\overrightarrow{OP}=x\overrightarrow{OD}+y\overrightarrow{OH}$，则x+y的最大值为4．