题目内容
14．
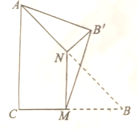如图，∠C=$\frac{π}{2}$，AC=BC，M，N分别是BC、AB的中点，沿直线MN将△BMN折起使点B到达B′，且∠B′MB=$\frac{π}{3}$，则B′A与平面ABC所成角的正切值为（ ）| A． | $\frac{\sqrt{2}}{5}$ | B． | $\frac{\sqrt{3}}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{5}$ |
分析 由题意画出图形，作出B′A在平面ABC上的投影，得到B′A与平面ABC所成角，求解直角三角形得答案．
解答 解：如图：
由于折叠之前BM与CM都始终垂直于MN，这在折叠之后仍然成立，
∴折叠之后平面B′MN与平面BMN所成的二面角即为∠B′MB=$\frac{π}{3}$，并且B′在底面ACB内的投影点H就在BC上，且恰在BM的中点位置，
连接B′A和AH，设AC=BC=a，
在直角三角形ACH中，AH=$\frac{5}{4}$a，
在直角三角形B′MH中，由于B′M=$\frac{1}{2}$a，∠B′MH=60°，∴B′H=$\frac{\sqrt{3}}{4}$a，
在直角三角形B′AH中，tan∠B′AH=$\frac{B′H}{AH}=\frac{\frac{\sqrt{3}}{4}a}{\frac{5}{4}a}=\frac{\sqrt{3}}{5}$．
故选：B．
点评 本题考查直线与平面所成的角，关键应抓住折叠前与折叠后的变量与不变量，考查了二面角的平面角及直线与平面所成角的概念，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．设f（x），g（x）是定义在同一区间[a，b]上的两个函数，若?x∈[a，b]都有|f（x）-g（x）|≤1成立，则称f（x），g（x）在[a，b]上是“亲密函数”，区间[a，b]称为“亲密区间”．若f（x）=x2+3x+2，g（x）=2x+1在[a，b]上是“亲密函数”，则其“亲密区间”是（ ）
| A． | [0，2] | B． | [0，1] | C． | [1，2] | D． | [-1，0] |
5．已知函数f（x）=x2+ax+b（a，b∈R）的图象与x轴相切，若直线y=c与y=c+5依次交f（x）的图象于A，B，C，D四点，且四边形ABCD的面积为25，则正实数c的值为（ ）
| A． | 4 | B． | 6 | C． | 2 | D． | 8 |
19．若a和b是计算机在区间（0，2）上产生的均匀随机数，则一元二次不等式ax2+4x+4b＞0（a＞0）的解集不是R的概率为（ ）
| A． | $\frac{1+2ln2}{4}$ | B． | $\frac{3-2ln2}{4}$ | C． | $\frac{1+ln2}{2}$ | D． | $\frac{1-ln2}{2}$ |
6．在四面体ABCD中，AB⊥AD，AB=AD=BC=CD=1，且平面ABD⊥平面BCD，M为AB中点，则CM与平面ABD所成角的正弦值为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC=90°，PA⊥面ABCD，若PA=AB=BC=$\frac{1}{2}$AD．