题目内容
4. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,PA⊥面ABCD,若PA=AB=BC=$\frac{1}{2}$AD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,PA⊥面ABCD,若PA=AB=BC=$\frac{1}{2}$AD.(1)求证:CD⊥平面PAC;
(2)侧棱PA上中点E,求证:BE∥平面PCD;
(3)求二面角A-PD-C的余弦值.
分析 (1)推导出PA⊥CD,AC⊥CD,由此能证明CD⊥平面PAC.
(2)取PD中点F,连结BE、EF、FC,推导出四边形BEFC为平行四边形,从而BE∥CF,由此能证明BE∥平面PCD.
(3)设G为AD的中点,连结CG,过G作GH⊥PD于H,连结CH,由三垂线定理得∠GHC是二面角A-PD-C的平面角,由此能求出二面角A-PD-C的余弦值.
解答 证明:(1)∵PA⊥底面ABCD,CD?底面ABCD,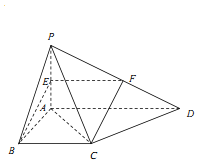
∴PA⊥CD,
在底面ABCD中,∵∠ABC=∠BAD=90°,AB=BC=$\frac{1}{2}AD$,
∴AC=CD=$\frac{\sqrt{2}}{2}AD$,∴AC⊥CD,
∵PA∩AC=A,∴CD⊥平面PAC.
(2)取PD中点F,连结BE、EF、FC,
则EF∥AD,且EF=$\frac{1}{2}AD$,
由已知∠ABC=∠BAD=90°,∴BC∥AD,
又BC=$\frac{1}{2}AD$,∴BC∥EF,且BC=EF,
∴四边形BEFC为平行四边形,∴BE∥CF,
∵BE?平面PCD,CF?平面PCD,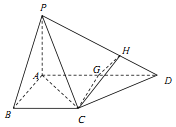
∴BE∥平面PCD.
解:(3)设G为AD的中点,连结CG,则CG⊥AD,
又∵平面ABCD⊥平面PAD,
∴CG⊥平面PAD,
过G作GH⊥PD于H,连结CH,
由三垂线定理得CH⊥PD,
∴∠GHC是二面角A-PD-C的平面角,
设AD=2,则PA=AB=CG=DG=1,DP=$\sqrt{5}$,
在△PAD中,$\frac{GH}{PA}=\frac{DG}{DP}$,∴GH=$\frac{1}{\sqrt{5}}$,
∴tan$∠GHC=\frac{CG}{GH}$=$\sqrt{5}$,cos$∠GHC=\frac{\sqrt{6}}{6}$.
∴二面角A-PD-C的余弦值为$\frac{\sqrt{6}}{6}$.
点评 本题考查线面垂直、线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 阅读快车系列答案
阅读快车系列答案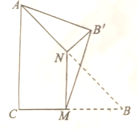 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
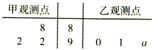 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.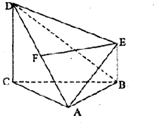 如图,四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.
如图,四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.