题目内容
19.若a和b是计算机在区间(0,2)上产生的均匀随机数,则一元二次不等式ax2+4x+4b>0(a>0)的解集不是R的概率为( )| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
分析 求出函数f(x)=ax2+4x+4b的值域为R(实数集),求出a,b的范围,再由几何概概型的概率公式,即可得到.
解答 解:由已知,a和b是计算机在区间(0,2)上产生的随机数,对应区域的面积为4,
要函数f(x)=ax2+4x+4b的定义域为R(实数集),则ax2+4x+4b恒为正,
∴△=16-16ab<0,即ab>1;
在平面直角坐标系中画出点(a,b)所在区域: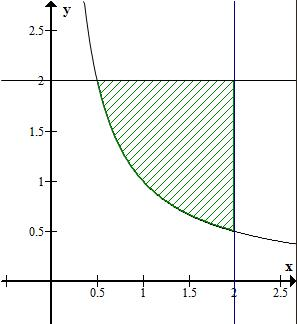
满足ab>1的区域面积为:${∫}_{\frac{1}{2}}^{2}$(2-$\frac{1}{x}$)dx=3-2ln2;
∴所求概率为P=1-$\frac{3-2ln2}{4}$=$\frac{1+2ln2}{4}$;
故选:A.
点评 本题考查的知识点是几何概型公式的运用,关键是要找出(0,2)上产生两个随机数a和b所对就图形的面积;
几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
13. 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )| A. | 4π | B. | 2π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
14.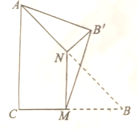 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
4.一个半径为$\sqrt{6}$的球的内接正四棱柱的高为4,则该正四棱柱的表面积为( )
| A. | 24 | B. | 32 | C. | 36 | D. | 40 |
8.已知函数f(x)=x2+mx+n,且y=f(x+2)的图象关于y轴对称,则大小关系正确的是( )
| A. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | B. | f(1)<f($\frac{7}{2}$)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
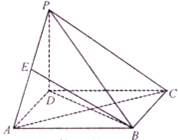 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,