题目内容
8.设f(x),g(x)是定义在同一区间[a,b]上的两个函数,若?x∈[a,b]都有|f(x)-g(x)|≤1成立,则称f(x),g(x)在[a,b]上是“亲密函数”,区间[a,b]称为“亲密区间”.若f(x)=x2+3x+2,g(x)=2x+1在[a,b]上是“亲密函数”,则其“亲密区间”是( )| A. | [0,2] | B. | [0,1] | C. | [1,2] | D. | [-1,0] |
分析 由“亲密函数”的概念知,?x∈[a,b]都有|f(x)-g(x)|=|x2+x+1|≤1成立,可求得f(x),g(x)的“亲密区间”是[-1,0],从而得到答案.
解答 解:若f(x)=x2+3x+2,g(x)=2x+1在[a,b]上是“亲密函数”,
则|f(x)-g(x)|=|x2+3x+2-(2x+1)|=|x2+x+1|≤1.
因为x2+x+1=(x+$\frac{1}{2}$)2+$\frac{3}{4}$>0,
所以,|x2+x+1|≤1?x2+x+1≤1,即x2+x≤0,
解得:-1≤x≤0.
即?x∈[-1,0]都有|f(x)-g(x)|≤1成立,f(x),g(x)的“亲密区间”是[-1,0].
故选:D.
点评 本题考查函数恒成立问题,理解新定义“亲密函数”与“亲密区间”是关键,考查推理与运算能力,属于中档题.

练习册系列答案
相关题目
19.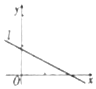 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )
 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),则下列结论正确的是( )| A. | x和y成正相关 | |
| B. | 若直线l方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,则$\widehat{b}$>0 | |
| C. | 最小二乘法是使尽量多的样本点落在直线上的方法 | |
| D. | 直线l过点$(\overline x,\overline y)$ |
16.已知集合A={1,2,3},B={-2,-1,0,1,2},则A∩B=( )
| A. | {1,2,3} | B. | {-2,-1,0,1,2} | C. | {1,2} | D. | {-2,-1} |
13. 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )| A. | 4π | B. | 2π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
14.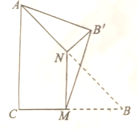 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
 如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )
如图,∠C=$\frac{π}{2}$,AC=BC,M,N分别是BC、AB的中点,沿直线MN将△BMN折起使点B到达B′,且∠B′MB=$\frac{π}{3}$,则B′A与平面ABC所成角的正切值为( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |