题目内容
下列命题中,正确的个数是( )
(1)?x∈N,x3>x2
(2)存在一个四边形没有外接圆
(3)每个对数函数都是单调函数
(4)任意素数都是奇数.
(1)?x∈N,x3>x2
(2)存在一个四边形没有外接圆
(3)每个对数函数都是单调函数
(4)任意素数都是奇数.
| A、2 | B、1 | C、4 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:可举反例x=1,即可判断(1);由圆内接四边形的特征,即可判断(2);由对数函数的单调性,即可判断(3);由素数的概念,举反例2,即可判断(4).
解答:
解:(1)当x=1时,x3=x2,故(1)错;
(2)由于圆内接四边形的对角互补,对角互补的四边形才有外接圆,故存在对角不互补的四边形没有外接圆,故(2)正确;
(3)形如y=logax(a>0,a≠1,x>0)的函数是对数函数,a>1,是(0,+∞)上的单调增函数,0<a<1,是(0,+∞)上的单调减函数,故(3)正确;
(4)素数是能被1和本身整除的数,2是素数,但2是偶数,故(4)错.
故正确的个数为2.
故选:A.
(2)由于圆内接四边形的对角互补,对角互补的四边形才有外接圆,故存在对角不互补的四边形没有外接圆,故(2)正确;
(3)形如y=logax(a>0,a≠1,x>0)的函数是对数函数,a>1,是(0,+∞)上的单调增函数,0<a<1,是(0,+∞)上的单调减函数,故(3)正确;
(4)素数是能被1和本身整除的数,2是素数,但2是偶数,故(4)错.
故正确的个数为2.
故选:A.
点评:本题考查全称性命题和存在性命题的真假,判断时注意举反例和运用性质加以验证,本题是一道基础题.

练习册系列答案
相关题目
若cos2t=-
cosxdx,其中t∈(0,π),则t=( )
| ∫ | t 0 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
若平面内两个向量
=(2cosθ,1)与
=(1,cosθ)共线,则cos2θ等于( )
| a |
| b |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
已知
≤k<1,函数f(x)=|2x-1|-k的零点分别为x1,x2(x1<x2),函数g(x)=|2x-1|-
的零点分别为x3,x4(x3<x4),则(x4-x3)+(x2-x1)的最小值为( )
| 1 |
| 3 |
| k |
| 2k+1 |
| A、1 |
| B、log23 |
| C、log26 |
| D、3 |
已知函数 f(x)=ax3+f′(2)x2+3,若 f′(1)=-5,则f′(2)=( )
| A、-l | B、-2 | C、-3 | D、-4 |
已知命题P:函数f(x)=
+lg(3-x)的定义域为(2,3),命题Q:已知
,
为非零向量,则“函数f(x)=(
x+
)2为偶函数”是“
⊥
”的充分但不必要条件.则下列命题为真命题的有( )
| 3x | ||
|
| a |
| b |
| a |
| b |
| a |
| b |
| A、P∧Q |
| B、P∧(¬Q) |
| C、(¬P)∧Q |
| D、(¬P)∨Q |
如图是甲,乙两名同学5次综合测评成绩的茎叶图,下列四个结论中,正确的是( )
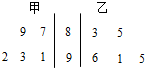

| A、甲成绩的极差大于乙成绩的极差 |
| B、甲成绩的中位数小于乙成绩的中位数 |
| C、甲成绩的平均值等于乙成绩的平均值 |
| D、甲成绩的标准差小于乙成绩的标准差 |