题目内容
15．数列{an}满足a1=0，an+1-an=2n，那么a2012的值是（ ）| A． | 2011×2010 | B． | 2012×2011 | C． | 20122 | D． | 2012×2013 |
分析 利用数列的递推关系式通过累加求和求解即可．
解答 解：数列{an}满足a1=0，an+1-an=2n，
可得a2-a1=2×1，
a3-a2=2×2，
a4-a3=2×3，
…
a2012-a2011=2×2011，
以上各式相加可得：a2012-a1=2×（1+2+3+…+2011）
=$2×\frac{1+2011}{2}$×2011
=2012×2011．
故选：B．
点评 本题考查数列的递推关系式的应用，数列累加法的应用，考查计算能力．
练习册系列答案
相关题目
20．
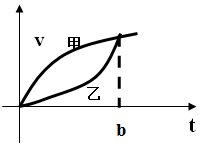甲、乙速度v与时间t的关系如图，a（b）是t=b时的加速度，S（b）是从t=0到t=b的路程，则a甲（b）与a乙（b），S甲（b）与S乙（b）的大小关系是（ ）
甲、乙速度v与时间t的关系如图，a（b）是t=b时的加速度，S（b）是从t=0到t=b的路程，则a甲（b）与a乙（b），S甲（b）与S乙（b）的大小关系是（ ）| A． | a甲（b）＞a乙（b），S甲（b）＞S乙（b） | B． | a甲（b）＜a乙（b），S甲（b）＜S乙（b） | ||
| C． | a甲（b）＜a乙（b），S甲（b）＞S乙（b） | D． | a甲（b）＜a乙（b），S甲（b）＜S乙（b） |
7．若变量x，y满足$\left\{{\begin{array}{l}{x+y≤2}\\{2x-3y≤9}\\{x≥0}\end{array}}\right.$则z=（x+1）2+y2的最大值是（ ）
| A． | 12 | B． | 10 | C． | 17 | D． | 26 |
4．《九章算术》中的“两鼠穿墙题”是我国数学的古典名题：“今有垣厚若干尺，两鼠对穿，大鼠日一尺，小鼠也日一尺．大鼠日自倍，小鼠日自半．问何日相逢，各穿几何？题意是：有两只老鼠从墙的两边打洞穿墙．大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半”如果墙足够厚，Sn为前n天两只老鼠打洞长度之和，则S5=（ ）
| A． | $31\frac{15}{16}$ | B． | $32\frac{15}{16}$ | C． | $33\frac{15}{16}$ | D． | $26\frac{1}{2}$ |