题目内容
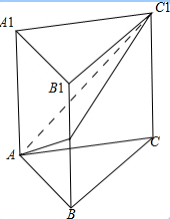如图，直三棱柱ABC-A1B1C中，AB⊥BC，AB=4，BC=6，AA1=8，有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1，并且在棱BB1上的一点M稍作停顿，当蚂蚁爬行距离最短时，BM的长度为考点：多面体和旋转体表面上的最短距离问题
专题：计算题,空间位置关系与距离
分析：将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1，与BB1的交点即为满足AM+MC1最小时的点M．
解答：
解：将直三棱柱ABC-A1B1C1沿棱BB1展开成平面连接AC1，与BB1的交点即为满足AM+MC1最小时的点M，
由于AB=4，BC=6，AA1=8，再结合棱柱的性质，可得
=
，
∴BM=3.2，
故答案为：3.2．
由于AB=4，BC=6，AA1=8，再结合棱柱的性质，可得
| BM |
| 8 |
| 4 |
| 10 |
∴BM=3.2，
故答案为：3.2．
点评：本题重点考查了棱柱的结构特征、侧面展开图等知识，属于中档题．
练习册系列答案
相关题目
已知函数y=f（x）对任意x∈R，恒有（f（x）-sinx）（f（x）-cosx）=0成立，则下列关于函数 y=f（x）的说法正确的是（ ）
| A、最小正周期是2π |
| B、值域是[-1，1] |
| C、是奇函数或是偶函数 |
| D、以上都不对 |
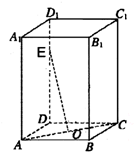如图，在长方体ABCD-A1B1C1D1中，O为AC的中点，设E是棱DD1上的点，且
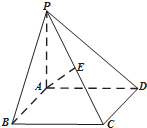如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，AB=2，AD=2