题目内容
已知a>0且a≠1,数列{an}是首项与公比均为a的等比数列,数列{bn}满足bn=an•lgan
(1)若a=3,求数列{bn}的前n项和Sn;
(2)若对于n∈N*,总有bn<bn+1,求a的取值范围.
(1)若a=3,求数列{bn}的前n项和Sn;
(2)若对于n∈N*,总有bn<bn+1,求a的取值范围.
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(1)由数列{an}是首项与公比均为a的等比数列,当a=3时,an=3n,可得bn=an•lgan=3nlg3n=n•3n.再利用“错位相减法”即可得出;
(2)数列{an}是首项与公比均为a的等比数列,a>0且a≠1,可得an=an.bn=an•lgan=n•an.由于对于n∈N*,总有bn<bn+1,可得a>
,由于数列{
}是单调递增数列,且
=1-
<1,即可得出.
(2)数列{an}是首项与公比均为a的等比数列,a>0且a≠1,可得an=an.bn=an•lgan=n•an.由于对于n∈N*,总有bn<bn+1,可得a>
| n |
| n+1 |
| n |
| n+1 |
| n |
| n+1 |
| 1 |
| n+1 |
解答:
解:(1)∵数列{an}是首项与公比均为a的等比数列,
∴当a=3时,an=3n,
bn=an•lgan=3nlg3n=n•3n.
∴数列{bn}的前n项和Sn=3+2×32+3×33+…+n•3n,
3Sn=32+2×33+…+(n-1)×3n+n×3n+1,
∴-2Sn=3+32+33+…+3n-n×3n+1=
-n×3n+1=
×3n+1-
,
∴Sn=
×3n+1+
.
(2)∵数列{an}是首项与公比均为a的等比数列,a>0且a≠1,
∴an=an.
∴bn=an•lgan=n•an.
∵对于n∈N*,总有bn<bn+1,
∴n•an<(n+1)•an+1,
∴a>
,
∵数列{
}是单调递增数列,且
=1-
<1,
∴a≥1.
∴a的取值范围是[1,+∞).
∴当a=3时,an=3n,
bn=an•lgan=3nlg3n=n•3n.
∴数列{bn}的前n项和Sn=3+2×32+3×33+…+n•3n,
3Sn=32+2×33+…+(n-1)×3n+n×3n+1,
∴-2Sn=3+32+33+…+3n-n×3n+1=
| 3(3n-1) |
| 3-1 |
| 1-2n |
| 2 |
| 3 |
| 2 |
∴Sn=
| 2n-1 |
| 4 |
| 3 |
| 4 |
(2)∵数列{an}是首项与公比均为a的等比数列,a>0且a≠1,
∴an=an.
∴bn=an•lgan=n•an.
∵对于n∈N*,总有bn<bn+1,
∴n•an<(n+1)•an+1,
∴a>
| n |
| n+1 |
∵数列{
| n |
| n+1 |
| n |
| n+1 |
| 1 |
| n+1 |
∴a≥1.
∴a的取值范围是[1,+∞).
点评:本题考查了等比数列的通项公式及其前n项和公式、“错位相减法”、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
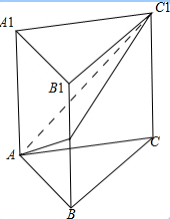 如图,直三棱柱ABC-A1B1C中,AB⊥BC,AB=4,BC=6,AA1=8,有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1,并且在棱BB1上的一点M稍作停顿,当蚂蚁爬行距离最短时,BM的长度为
如图,直三棱柱ABC-A1B1C中,AB⊥BC,AB=4,BC=6,AA1=8,有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1,并且在棱BB1上的一点M稍作停顿,当蚂蚁爬行距离最短时,BM的长度为