题目内容
11.在菱形ABCD中,A=60°,AB=$\sqrt{3}$,将△ABD沿BD折起到△PBD的位置,若二面角P-BD-C的大小为$\frac{2π}{3}$,则三棱锥P-BCD的外接球体积为( )| A. | $\frac{4}{3}$π | B. | $\frac{\sqrt{3}}{2}$π | C. | $\frac{7\sqrt{7}}{6}$π | D. | $\frac{7\sqrt{7}}{2}$π |
分析 取BD中点E,连接AE,CE,则∠AEC=$\frac{2π}{3}$,AE=CE=$\frac{3}{2}$,建立方程组,求出三棱锥P-BCD的外接球的半径,即可求出三棱锥P-BCD的外接球体积.
解答 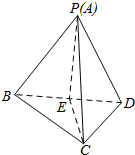 解:取BD中点E,连接AE,CE,则∠PEC=$\frac{2π}{3}$,PE=CE=$\frac{3}{2}$
解:取BD中点E,连接AE,CE,则∠PEC=$\frac{2π}{3}$,PE=CE=$\frac{3}{2}$
设△BCD的外接圆的圆心与球心的距离为h,
三棱锥P-BCD的外接球的半径为R,则$\left\{\begin{array}{l}{{R}^{2}=1+{h}^{2}}\\{(\frac{3\sqrt{3}}{4}-h)^{2}+(\frac{5}{4})^{2}={R}^{2}}\end{array}\right.$,
∴R=$\frac{\sqrt{7}}{2}$,h=$\frac{\sqrt{3}}{2}$,
∴三棱锥P-BCD的外接球体积为$\frac{4}{3}π•(\frac{\sqrt{7}}{2})^{3}$=$\frac{7\sqrt{7}}{6}π$.
故选:C.
点评 本题考查三棱锥P-BCD的外接球体积,考查学生的计算能力,确定三棱锥P-BCD的外接球的半径是关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
6.若存在斜率且过点P(-1,-$\frac{b}{a}$)的直线l与双曲线:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$有且仅有一个公共点,且这个公共点恰是双曲线的左顶点,则双曲线的实轴长等于( )
| A. | 2 | B. | 4 | C. | 1或2 | D. | 2或4 |
3.长方体长、宽、高分别为2、2、4,则它的体积等于( )
| A. | 4 | B. | 8 | C. | 16 | D. | $\frac{16}{3}$ |
20.判断直线(a-1)x+y+a-3=0与圆x2+y2-4y=0的位置关系( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 无法判断 |
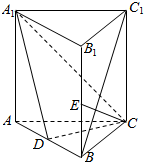 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.