题目内容
已知数列{bn},bn=
bn-1,求bn的前n项和Sn.
| 1 |
| 2 |
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由已知得{bn}是首项为b1,公式为
的等比数列,由此能求出其前n项和Sn.
| 1 |
| 2 |
解答:
解:∵数列{bn},bn=
bn-1,
∴{bn}是首项为b1,公式为
的等比数列,
∴bn的前n项和Sn=
=2b1-
.
| 1 |
| 2 |
∴{bn}是首项为b1,公式为
| 1 |
| 2 |
∴bn的前n项和Sn=
b1(1-
| ||
1-
|
| 1 |
| 2n-1 |
点评:本题考查数列的前n项和的求法,是基础题,解题时要注意等比数列的性质的合理运用.

练习册系列答案
相关题目
为了得到函数y=cos(2x+1)的图象,只需将函数y=cos2x的图象上所有的点( )
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移1个单位长度 | ||
| D、向右平移1个单位长度 |
已知一个算法的流程图如图所示,则输出的结果是( )
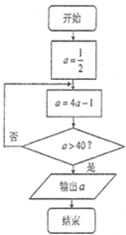

| A、3 | B、11 | C、43 | D、171 |
等差数列{an}的前n项和为Sn,若a2+a5+a8=15,a2+a4+a6=12,则S8的值是( )
| A、21 | B、24 | C、36 | D、7 |