题目内容
在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,△ABC的面积为3
,b=4,c=3,则△ABC的外接圆的直径为 .
| 3 |
考点:正弦定理
专题:解三角形
分析:由已知及三角形面积公式可解得sinA,已知△ABC是锐角三角形,可得cosA=
,由余弦定理可解得a,由正弦定理可得2R的值.
| 1 |
| 2 |
解答:
解:∵由已知及三角形面积公式可得:3
=
×4×3×sinA,
∴可解得:sinA=
,
∴已知△ABC是锐角三角形,可得:cosA=
=
,
∴由余弦定理知:a2=b2+c2-2bccosA=16+9-12=13,可解得:a=
,
∴由正弦定理可得:2R=
=
=
.
故答案为:
.
| 3 |
| 1 |
| 2 |
∴可解得:sinA=
| ||
| 2 |
∴已知△ABC是锐角三角形,可得:cosA=
| 1-sin2A |
| 1 |
| 2 |
∴由余弦定理知:a2=b2+c2-2bccosA=16+9-12=13,可解得:a=
| 13 |
∴由正弦定理可得:2R=
| a |
| sinA |
| ||||
|
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题主要考查了三角形面积公式,正弦定理,余弦定理的应用,属于基本知识的考查.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知函数f(x)=
,若|f(x)|≥a(x-1),则a的取值范围是( )
|
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,1] |
| D、[-1,0] |
下列结论中正确的是( )
| A、“x≠1”是“x(x-1)≠0”的充分不必要条件 |
| B、已知随机变量ξ服从正态分布N(5,1),且P(4≤ξ≤6)=0.7,则P(ξ>6)=0.15 |
| C、将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化 |
| D、某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了解该单位职工的健康情况,应采用系统抽样的方法从中抽取样本 |
将函数f(x)=sin(x+
)的图象向右平移φ(φ>0)个单位长度,得到的曲线经过原点,则φ的最小值为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
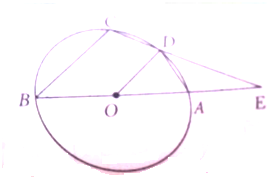 如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.
如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC. 在等腰直角三角形ABC中,AB=AC=1,点P是边AB上异于A、B的一点,光线从点P出发,经BC、CA反射后又回到点P(如图所示),若光线QR经过△ABC的重心,则AP=( )
在等腰直角三角形ABC中,AB=AC=1,点P是边AB上异于A、B的一点,光线从点P出发,经BC、CA反射后又回到点P(如图所示),若光线QR经过△ABC的重心,则AP=( )