题目内容
函数y=2tanx+a在x∈[
，
]上的最大值为4，则实数a为 ．
| π |
| 6 |
| π |
| 3 |
考点：正切函数的图象
专题：三角函数的图像与性质
分析：根据正切函数的单调性和最值建立方程关系即可．
解答：
解：∵函数y=2tanx+a在x∈[
，
]上为增函数，
∴当x=
时，函数y=2tanx+a确定最大值为4，
即在2tan
+a=4，
即a=4-2
，
故答案为：4-2
| π |
| 6 |
| π |
| 3 |
∴当x=
| π |
| 3 |
即在2tan
| π |
| 3 |
即a=4-2
| 3 |
故答案为：4-2
| 3 |
点评：本题主要考查正切函数的图象和性质，利用三角函数的单调性和最值的性质是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=log2（x-1）的定义域是（ ）
| A、{x∈R|x＞1} |
| B、{x∈R|x＜1} |
| C、{x∈R|x≥1} |
| D、{x∈R|x≤1} |
命题“若x∈N*，则x2≥0”的逆命题，否命题，逆否命题中，正确的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
已知偶函数f（x）在区间（0，+∞）上单调递减，且a=f（-1），b=f（log24），则实数a，b的大小关系时（ ）
| A、a＜b | B、a=b |
| C、a＞b | D、不能比较 |
圆x2+y2+2x+4y-2=0上到直线x+y+1=0的距离为
的点个数为（ ）
| ||
| 2 |
| A、1 | B、2 | C、3 | D、4 |
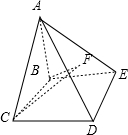如图，在空间图形A-BCDE中，AB⊥平面BCDE，底面BCDE是直角梯形，且∠CBE=90°，BC∥DE，AB=DE=BE=