题目内容
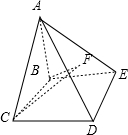 如图,在空间图形A-BCDE中,AB⊥平面BCDE,底面BCDE是直角梯形,且∠CBE=90°,BC∥DE,AB=DE=BE=
如图,在空间图形A-BCDE中,AB⊥平面BCDE,底面BCDE是直角梯形,且∠CBE=90°,BC∥DE,AB=DE=BE=| 1 |
| 2 |
考点:异面直线及其所成的角
专题:空间角
分析:以B为原点,BC为x轴,BE为y轴,BA为z轴,建立空间直角坐标系,点C在平面ADE内的射影为点F,由向量法求出F(2,
,
),由此能求出异面直线BF与CD所成角的大小.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:以B为原点,BC为x轴,BE为y轴,BA为z轴,
建立空间直角坐标系,
由已知得B(0,0,0),C(2,0,0),
D(1,1,0),E(0,1,0),A(0,0,1),
=(1,1,-1),
=(0,1,-1),
设F(a,b,c),
则
=(a,b,c-1),
=(a-2,b,c),
∵点C在平面ADE内的射影为点F,
∴
是平面ADE的法向量,
∴
,
解得a=2,b=c=
,
∴F(2,
,
),∴
=(2,
,
),
=(-1,1,0),
|cos<
,
>|=|
|=|
|=
,
∴异面直线BF与CD所成角的大小为60°.

建立空间直角坐标系,
由已知得B(0,0,0),C(2,0,0),
D(1,1,0),E(0,1,0),A(0,0,1),
| AD |
| AE |
设F(a,b,c),
则
| AF |
| CF |
∵点C在平面ADE内的射影为点F,
∴
| CF |
∴
|
解得a=2,b=c=
| 1 |
| 2 |
∴F(2,
| 1 |
| 2 |
| 1 |
| 2 |
| BF |
| 1 |
| 2 |
| 1 |
| 2 |
| CD |
|cos<
| BF |
| CD |
| ||||
|
|
-2+
| ||||||
|
| 1 |
| 2 |
∴异面直线BF与CD所成角的大小为60°.
点评:本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
要得到函数y=cos(
-
)的图象,只需将函数y=sin
的图象上所有点( )
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
在关于x的不等式x2-(a+1)x+a<0的解集中恰有两个整数,则a的取值范围是( )
| A、(3,4) |
| B、(-2,-1)∪(3,4) |
| C、(3,4] |
| D、[-2,-1)∪(3,4] |
在△ABC中,角A,B,C的对边分别为a,b,c.已知(a-c)(sinA+sinC)=(b-c)sinB,则角A的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,某渠道的截面是一个等腰梯形,上底 AD长为一腰和下底长之和,且两腰 A B,CD与上底 AD之和为8米,试问:等腰梯形的腰与上、下底长各为多少时,截面面积最大?并求出截面面积S的最大值.
如图,某渠道的截面是一个等腰梯形,上底 AD长为一腰和下底长之和,且两腰 A B,CD与上底 AD之和为8米,试问:等腰梯形的腰与上、下底长各为多少时,截面面积最大?并求出截面面积S的最大值.