题目内容
保持正弦曲线上所有点的纵坐标不变,横坐标缩短为原来的
,再将图象沿x轴向右平移
个单位,得到函数f(x)的图象.
(1)写出f(x)的表达式,并计算f(
).
(2)求出f(x)在[
,
π]上的值域.
| 1 |
| 2 |
| π |
| 6 |
(1)写出f(x)的表达式,并计算f(
| π |
| 2 |
(2)求出f(x)在[
| π |
| 3 |
| 3 |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)根据函数y=Asin(ωx+φ)的图象变换规律求得f(x)的表达式,并计算f(
)的值.
(2)由条件利用正弦函数的定义域和值域,求得f(x)在[
,
π]上的值域.
| π |
| 2 |
(2)由条件利用正弦函数的定义域和值域,求得f(x)在[
| π |
| 3 |
| 3 |
| 4 |
解答:
解:(1)把y=sinx的图象上所有点的纵坐标不变,横坐标缩短为原来的
,可得y=sin2x的图象;
再将图象沿x轴向右平移
个单位,可得函数y=sin2(x-
)=sin(2x-
)的图象,
故有 f(x)=sin(2x-
),∴f(
)=sin(π-
)=sin
=
.
(2)∵x∈[
,
π],∴2x∈[
,
π],∴2x-
∈[
,
],sin(2x-
)∈[-
,1],
即f(x)在[
,
π]上的值域为[-
,1].
| 1 |
| 2 |
再将图象沿x轴向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
故有 f(x)=sin(2x-
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
(2)∵x∈[
| π |
| 3 |
| 3 |
| 4 |
| 2π |
| 3 |
| 3 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
即f(x)在[
| π |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC中,向量
=
,向量
=
,向量
=
.|
|=3,|
|=3,|
|=5,则
•
+
•
+
•
=( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
A、-
| ||
| B、22 | ||
| C、-22 | ||
D、
|
 已知函数y=2|x|,x∈R
已知函数y=2|x|,x∈R 已知函数f(x)=2x+1,g(x)=x2-2x+1.
已知函数f(x)=2x+1,g(x)=x2-2x+1.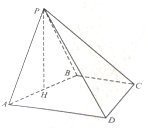 如图,四棱锥P-ABCD,底面ABCD为直角梯形,BC∥AD,BC⊥CD,BC=CD=
如图,四棱锥P-ABCD,底面ABCD为直角梯形,BC∥AD,BC⊥CD,BC=CD=