题目内容
已知圆C:x2+y2=4,直线l:y-kx+2=0
(1)k=1时判断圆C和直线的位置关系.
(2)若圆C上有且仅有三个点到l的距离为1,求实数k的值.
(1)k=1时判断圆C和直线的位置关系.
(2)若圆C上有且仅有三个点到l的距离为1,求实数k的值.
考点:直线与圆的位置关系,直线与圆相交的性质
专题:直线与圆
分析:(1)k=1时,直线l:y-x+2=0,利用圆心到直线的距离和圆半径的大小关系能判断直线和圆的位置关系.
(2)要满足条件“圆C上有且仅有三个点到直线l距离为”,当圆心C到直线l的距离为时即可.
(2)要满足条件“圆C上有且仅有三个点到直线l距离为”,当圆心C到直线l的距离为时即可.
解答:
解:(1)k=1时,直线l:y-x+2=0,
圆C:x2+y2=4的圆心C(0,0),半径r=2,
圆心C(0,0)到直线l的距离:
d=
=
<r=2,
∴k=1时圆C和直线相交.
(2)∵圆C:x2+y2=4,直线l:y-kx+2=0,
圆C上有且仅有三个点到l的距离为1,
∴圆心C(0,0)到直线直线l:y-kx+2=0的距离为1,
∴
=1,解得k=±
.
圆C:x2+y2=4的圆心C(0,0),半径r=2,
圆心C(0,0)到直线l的距离:
d=
| |2| | ||
|
| 2 |
∴k=1时圆C和直线相交.
(2)∵圆C:x2+y2=4,直线l:y-kx+2=0,
圆C上有且仅有三个点到l的距离为1,
∴圆心C(0,0)到直线直线l:y-kx+2=0的距离为1,
∴
| |2| | ||
|
| 3 |
点评:本题考查直线与圆的位置关系的判断,考查实数值的求法,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
不等式(x+5)(3-2x)≥6的解集是( )
A、(-∞,-1)∪[
| ||
B、[-1,
| ||
C、(-∞,-
| ||
D、[-
|





 如图,在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD. 在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,PB=2
在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,PB=2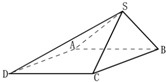 如图,设四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=
如图,设四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=