Question

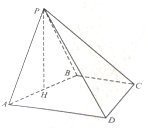如图，四棱锥P-ABCD，底面ABCD为直角梯形，BC∥AD，BC⊥CD，BC=CD=

1

2

AD．△APB是等腰三角形，∠APB=90°，H是AB中点，PC=PD．
（Ⅰ）证明：PH⊥平面ABCD；
（Ⅱ）求平面PCD与平面PBC所成锐二面角的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）取CD中点G，连接PG，HG，证明PH⊥AB，CD⊥PH，利用线面垂直的判定定理证明PH⊥平面ABCD；
（Ⅱ）建立如图所示的空间直角坐标系，求出平面PBC的法向量、平面PDC的一个法向量，利用向量的夹角公式求平面PCD与平面PBC所成锐二面角的余弦值．

解答： （Ⅰ）证明：取CD中点G，连接PG，HG．
∵PC=PD，CD中点G，
∴PG⊥CD．
∵△APB是等腰直角三角形，H是AB中点，
∴PH⊥AB，HG∥AD．∵BC∥AD，BC⊥CD，
∴HG⊥CD，…（4分）
HG∩PG=G，HG?平面PHG，PG?平面PHG，
∴CD⊥平面PHG．PH?平面PHG，∴CD⊥PH．
∵AB?平面ABCD，CD?平面ABCD，AB和CD相交，
∴PH⊥平面ABCD．                                        …（6分）
（Ⅱ）解：连接BD，由勾股定理可知AB⊥BD．建立如图所示的空间直角坐标系，设BC=CD=

1

2

AD=2
则点B（0，0，0），D（0，2

2

，0），C（-

2

，

2

，0），P（

2

，0，

2

），…（8分）
设平面PBC的法向量

m

=（x，y，z），则
∵

BC

=（-

2

，

2

，0），

PC

=（-2

2

，

2

，-

2

），
∴

-2 2 x+ 2 y- 2 z=0 - 2 x+ 2 y=0

．
∴平面PBC的一个法向量为

m

=（1，1，-1）．
同理平面PDC的一个法向量为

n

=（1，-1，-3）…（10分）
∴cos＜

m

，

n

＞=

1-1+3

3 • 11

=

33

11

                …（12分）

点评：本题主要考查四棱锥的有关知识，涉及线面、面面位置关系的判定与证明，还有二面角的计算．高考立体几何综合题大都以棱柱和棱锥为载体，综合考查空间想象能力和分析、解决问题的能力．空间角的计算一般有传统法和坐标向量法两种基本方法，前者着重思维，后者重在向量的坐标运算，各有优点，解题时既要具体问题具体分析，又要考虑到考生本人对这两种方法掌握的熟练程度而定．