题目内容
已知a,b为异面直线,则下列命题中正确的是( )
| A、过a,b外一点P一定可以引一条与a,b都平行的直线 |
| B、过a,b外一点P一定可以作一个与a,b都平行的平面 |
| C、过a一定可以作一个与b平行的平面 |
| D、过a一定可以作一个与b垂直的平面 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:A用反证法说明a,b为异面直线时,过a,b外一点P引一条直线l与a,b不能都平行;
B当a、b为异面直线时,过两直线外一点p作平面,该平面可能与a、b都平行,这样的平面也可能不存在;
C当a、b为异面直线时,过a作与b平行的平面有且只有一个;
D当a、b为异面直线时,过a作一个平面可能与b垂直,也可能与b不垂直.
B当a、b为异面直线时,过两直线外一点p作平面,该平面可能与a、b都平行,这样的平面也可能不存在;
C当a、b为异面直线时,过a作与b平行的平面有且只有一个;
D当a、b为异面直线时,过a作一个平面可能与b垂直,也可能与b不垂直.
解答:
解:对于A,当a,b为异面直线,假设过a,b外一点P引一条直线l与a,b都平行,
即l∥a,l∥b,∴a∥b,这与a、b是异面直线矛盾,∴假设不成立,即A错误;
对于B,∵a、b为异面直线,∴a、b 不平行,
∴过p做a的平行线有且只有一条,设为c,过p做b的平行线有且只有一条设为d,
则a、b的平行线只能组成一个平面,设为平面A;
①如果c恰好和b相交 或者 d与a相交,即当a或者b正好在A平面内时,过P且与a、b都平行的平面不存在;
②如果c不与b相交 或者 d不与a相交,过P且与a、b都平行的平面有且只有一个;∴B错误;
对于C,∵a、b为异面直线,∴a、b 不平行,在a上任取一点P,过点P作直线c∥b,c是唯一的,
又a∩c=P,∴由a、c确定的平面α也是唯一的,∴b∥α,∴C正确;
对于D,∵a、b为异面直线,但a与b不一定垂直,
∴过a作一个平面可能与b垂直,也可能与b平行,∴D错误.
故选:C.
即l∥a,l∥b,∴a∥b,这与a、b是异面直线矛盾,∴假设不成立,即A错误;
对于B,∵a、b为异面直线,∴a、b 不平行,
∴过p做a的平行线有且只有一条,设为c,过p做b的平行线有且只有一条设为d,
则a、b的平行线只能组成一个平面,设为平面A;
①如果c恰好和b相交 或者 d与a相交,即当a或者b正好在A平面内时,过P且与a、b都平行的平面不存在;
②如果c不与b相交 或者 d不与a相交,过P且与a、b都平行的平面有且只有一个;∴B错误;
对于C,∵a、b为异面直线,∴a、b 不平行,在a上任取一点P,过点P作直线c∥b,c是唯一的,
又a∩c=P,∴由a、c确定的平面α也是唯一的,∴b∥α,∴C正确;
对于D,∵a、b为异面直线,但a与b不一定垂直,
∴过a作一个平面可能与b垂直,也可能与b平行,∴D错误.
故选:C.
点评:本题考查了空间中的位置关系的应用问题.考查了异面直线的概念与应用问题,也考查了空间中的平行与垂直的判断问题,是综合题目.

练习册系列答案
相关题目
已知a>0,b>0,3是3a与32b等比中项,
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、4 | ||||
B、3+2
| ||||
C、
| ||||
| D、2 |
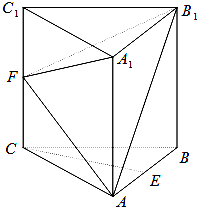 如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.
如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.