题目内容
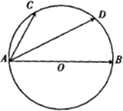
如图,AB是⊙O的直径,点C,D是半圆弧AB上的两个三等分点,
=
,
=
,则
=( )
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:向量在几何中的应用
专题:平面向量及应用
分析:连结CD、OD,由圆的性质与等腰三角形的性质,证出CD∥AB且AC∥DO,得到四边形ACDO为平行四边形,再根据题设条件即可得到用表示向量的式子.
解答:
解:连结CD、OD,
∵点C、D是半圆弧AB的两个三等分点,
∴
=
,可得CD∥AB,∠CAD=∠DAB=
×90°=30°,
∵OA=OD
∴∠ADO=∠DAO=30°,
由此可得∠CAD=∠DAO=30°,
∴AC∥DO.
∴四边形ACDO为平行四边形,
∴
=
+
=
+
=
+
,
故选:A
∵点C、D是半圆弧AB的两个三等分点,
∴
 |
| AC |
 |
| BD |
| 1 |
| 3 |
∵OA=OD
∴∠ADO=∠DAO=30°,
由此可得∠CAD=∠DAO=30°,
∴AC∥DO.
∴四边形ACDO为平行四边形,
∴
| AD |
| AO |
| AC |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| a |
| b |
故选:A
点评:本题给出半圆弧的三等分点,求向量的线性表示式.着重考查了圆周角定理、平行四边形的判定与向量的线性运算等知识,属于中档题.

练习册系列答案
相关题目
设U=R全集,集合A={y|y=x2+1},B={x|x2-2x-3≥0},则A∩(∁UB)=( )
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1<x≤1} |
| D、{x|1≤x<3} |
